Nota
Fare clic qui per scaricare il codice di esempio completo
Esercitazione sull'immagine #
Un breve tutorial sulla stampa di immagini con Matplotlib.
Comandi di avvio #
Innanzitutto, avviamo IPython. È un eccellente miglioramento del prompt Python standard e si lega particolarmente bene a Matplotlib. Avvia IPython direttamente su una shell o con Jupyter Notebook (dove IPython è un kernel in esecuzione).
Con IPython avviato, ora dobbiamo connetterci a un ciclo di eventi della GUI. Questo dice a IPython dove (e come) visualizzare i grafici. Per connetterti a un loop della GUI, esegui %matplotlib magic al prompt di IPython. Ci sono maggiori dettagli su cosa esattamente fa nella documentazione di IPython sui loop di eventi della GUI .
Se stai usando Jupyter Notebook, sono disponibili gli stessi comandi, ma le persone usano comunemente un argomento specifico per %matplotlib magic:
In [1]: %matplotlib inline
Questo attiva il plottaggio in linea, dove la grafica della trama apparirà nel tuo taccuino. Questo ha importanti implicazioni per l'interattività. Per il tracciato in linea, i comandi nelle celle al di sotto della cella che emette un tracciato non influiranno sul tracciato. Ad esempio, non è possibile modificare la mappa dei colori dalle celle sotto la cella che crea un grafico. Tuttavia, per altri backend, come Qt, che aprono una finestra separata, le celle al di sotto di quelle che creano la trama cambieranno la trama: è un oggetto vivo in memoria.
Questo tutorial utilizzerà l'interfaccia di tracciamento implicita di Matplotlib, pyplot. Questa interfaccia mantiene lo stato globale ed è molto utile per sperimentare rapidamente e facilmente varie impostazioni di trama. L'alternativa è quella esplicita, più adatta allo sviluppo di applicazioni di grandi dimensioni. Per una spiegazione dei compromessi tra le interfacce implicite ed esplicite, vedere Matplotlib Application Interfaces (API) e la Guida rapida per iniziare a utilizzare l'interfaccia esplicita. Per ora, andiamo avanti con l'approccio implicito:
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
Importazione dei dati dell'immagine negli array Numpy #
Matplotlib si affida alla libreria Pillow per caricare i dati dell'immagine.
Ecco l'immagine con cui giocheremo:

È un'immagine PNG RGB a 24 bit (8 bit per ciascuno di R, G, B). A seconda di dove ottieni i tuoi dati, gli altri tipi di immagine che molto probabilmente incontrerai sono immagini RGBA, che consentono la trasparenza o immagini in scala di grigi (luminosità) a canale singolo. Scarica stinkbug.png sul tuo computer per il resto di questo tutorial.
Ed eccoci qua...
img = mpimg.imread('../../doc/_static/stinkbug.png')
print(img)
[[[0.40784314 0.40784314 0.40784314]
[0.40784314 0.40784314 0.40784314]
[0.40784314 0.40784314 0.40784314]
...
[0.42745098 0.42745098 0.42745098]
[0.42745098 0.42745098 0.42745098]
[0.42745098 0.42745098 0.42745098]]
[[0.4117647 0.4117647 0.4117647 ]
[0.4117647 0.4117647 0.4117647 ]
[0.4117647 0.4117647 0.4117647 ]
...
[0.42745098 0.42745098 0.42745098]
[0.42745098 0.42745098 0.42745098]
[0.42745098 0.42745098 0.42745098]]
[[0.41960785 0.41960785 0.41960785]
[0.41568628 0.41568628 0.41568628]
[0.41568628 0.41568628 0.41568628]
...
[0.43137255 0.43137255 0.43137255]
[0.43137255 0.43137255 0.43137255]
[0.43137255 0.43137255 0.43137255]]
...
[[0.4392157 0.4392157 0.4392157 ]
[0.43529412 0.43529412 0.43529412]
[0.43137255 0.43137255 0.43137255]
...
[0.45490196 0.45490196 0.45490196]
[0.4509804 0.4509804 0.4509804 ]
[0.4509804 0.4509804 0.4509804 ]]
[[0.44313726 0.44313726 0.44313726]
[0.44313726 0.44313726 0.44313726]
[0.4392157 0.4392157 0.4392157 ]
...
[0.4509804 0.4509804 0.4509804 ]
[0.44705883 0.44705883 0.44705883]
[0.44705883 0.44705883 0.44705883]]
[[0.44313726 0.44313726 0.44313726]
[0.4509804 0.4509804 0.4509804 ]
[0.4509804 0.4509804 0.4509804 ]
...
[0.44705883 0.44705883 0.44705883]
[0.44705883 0.44705883 0.44705883]
[0.44313726 0.44313726 0.44313726]]]
Nota il dtype lì - float32. Matplotlib ha ridimensionato i dati a 8 bit da ciascun canale a dati in virgola mobile tra 0.0 e 1.0. Come nota a margine, l'unico tipo di dati con cui Pillow può lavorare è uint8. Il tracciato Matplotlib può gestire float32 e uint8, ma la lettura/scrittura di immagini per qualsiasi formato diverso da PNG è limitata ai dati uint8. Perché 8 bit? La maggior parte dei display può eseguire il rendering solo di 8 bit per canale di gradazione di colore. Perché possono rendere solo 8 bit/canale? Perché questo è tutto ciò che l'occhio umano può vedere. Altro qui (dal punto di vista della fotografia): Tutorial sulla profondità di bit del paesaggio luminoso .
Ciascun elenco interno rappresenta un pixel. Qui, con un'immagine RGB, ci sono 3 valori. Poiché si tratta di un'immagine in bianco e nero, R, G e B sono tutti simili. Un RGBA (dove A è alfa o trasparenza), ha 4 valori per elenco interno e una semplice immagine di luminanza ha solo un valore (ed è quindi solo un array 2-D, non un array 3-D). Per le immagini RGB e RGBA, Matplotlib supporta i tipi di dati float32 e uint8. Per la scala di grigi, Matplotlib supporta solo float32. Se i dati dell'array non soddisfano una di queste descrizioni, è necessario ridimensionarli.
Tracciare array numpy come immagini #
Quindi, hai i tuoi dati in un array numpy (importandolo o generandolo). Rendiamolo. In Matplotlib, questo viene eseguito utilizzando la imshow()funzione. Qui prenderemo l'oggetto della trama. Questo oggetto ti offre un modo semplice per manipolare la trama dal prompt.
imgplot = plt.imshow(img)
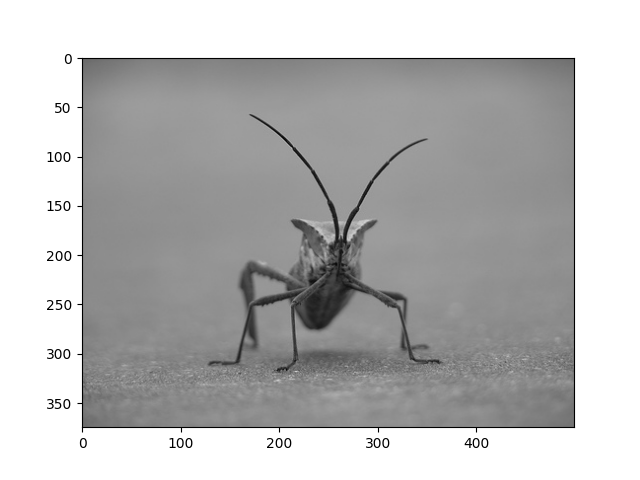
Puoi anche tracciare qualsiasi array numpy.
Applicazione di schemi di pseudocolori ai grafici delle immagini #
Lo pseudocolore può essere uno strumento utile per migliorare il contrasto e visualizzare più facilmente i dati. Ciò è particolarmente utile quando si effettuano presentazioni dei dati utilizzando i proiettori: il loro contrasto è in genere piuttosto scarso.
Lo pseudocolore è rilevante solo per le immagini di luminosità a canale singolo, in scala di grigi. Al momento abbiamo un'immagine RGB. Poiché R, G e B sono tutti simili (guarda tu stesso sopra o nei tuoi dati), possiamo semplicemente scegliere un canale dei nostri dati:
lum_img = img[:, :, 0]
# This is array slicing. You can read more in the `Numpy tutorial
# <https://numpy.org/doc/stable/user/quickstart.html>`_.
plt.imshow(lum_img)
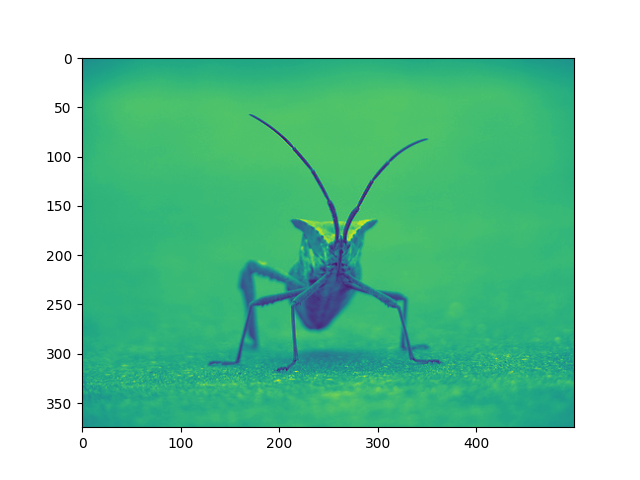
<matplotlib.image.AxesImage object at 0x7f2cdd608610>
Ora, con un'immagine di luminosità (2D, senza colore), viene applicata la mappa dei colori predefinita (nota anche come tabella di ricerca, LUT). L'impostazione predefinita si chiama viridis. Ci sono molti altri tra cui scegliere.
plt.imshow(lum_img, cmap="hot")
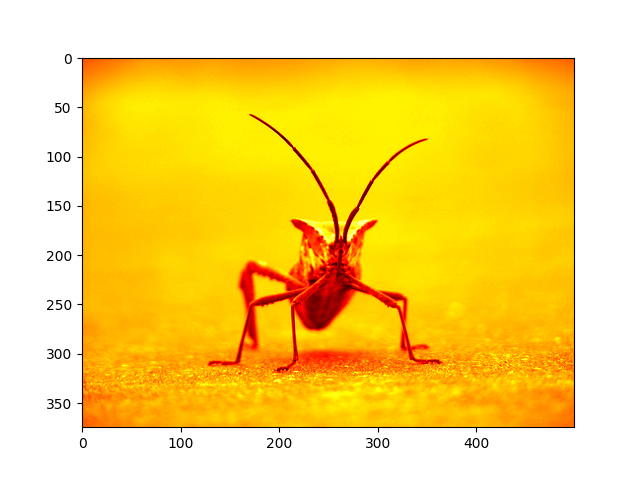
<matplotlib.image.AxesImage object at 0x7f2cddcc2aa0>
Si noti che è anche possibile modificare le mappe dei colori sugli oggetti di stampa esistenti utilizzando il
set_cmap()metodo:
imgplot = plt.imshow(lum_img)
imgplot.set_cmap('nipy_spectral')
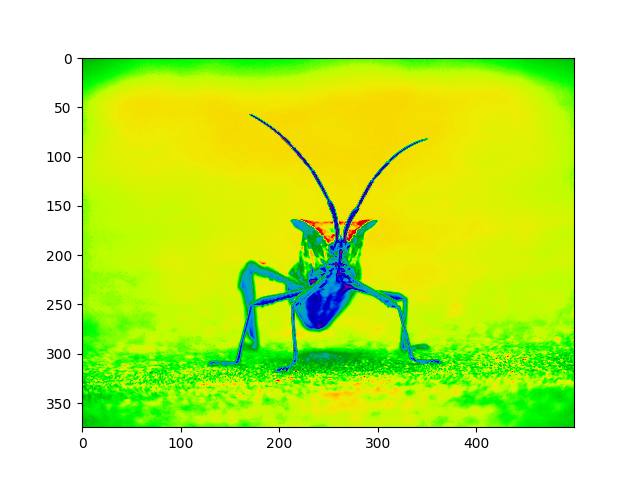
Nota
Tuttavia, ricorda che in Jupyter Notebook con il back-end inline non puoi apportare modifiche ai grafici di cui è già stato eseguito il rendering. Se crei imgplot qui in una cella, non puoi chiamare set_cmap() su di esso in una cella successiva e aspettarti che il grafico precedente cambi. Assicurati di inserire questi comandi insieme in una cella. I comandi plt non cambieranno i grafici delle celle precedenti.
Ci sono molti altri schemi Colormap disponibili. Vedi l' elenco e le immagini dei Colormaps .
Riferimento scala colori #
È utile avere un'idea del valore che rappresenta un colore. Possiamo farlo aggiungendo una barra colorata alla tua figura:
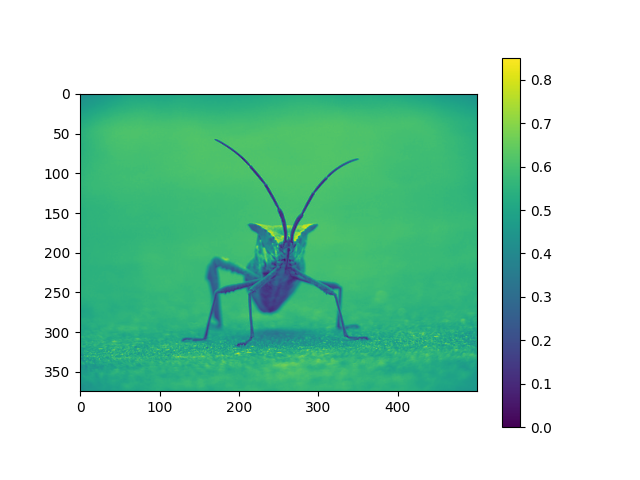
<matplotlib.colorbar.Colorbar object at 0x7f2cdf5297e0>
Esame di un intervallo di dati specifico #
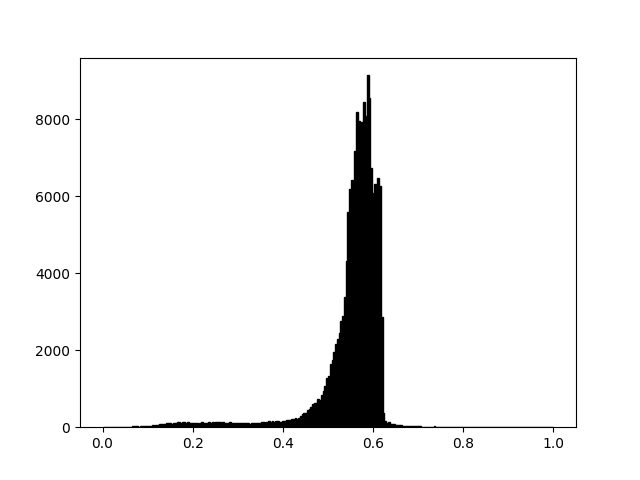
A volte vuoi migliorare il contrasto nella tua immagine o espandere il contrasto in una particolare regione, sacrificando i dettagli nei colori che non variano molto o non contano. Un buon strumento per trovare regioni interessanti è l'istogramma. Per creare un istogramma dei nostri dati immagine, utilizziamo la hist()funzione.
(array([2.000e+00, 2.000e+00, 3.000e+00, 3.000e+00, 2.000e+00, 2.000e+00,
3.000e+00, 1.000e+00, 7.000e+00, 9.000e+00, 7.000e+00, 2.000e+00,
7.000e+00, 1.000e+01, 1.100e+01, 1.500e+01, 1.400e+01, 2.700e+01,
2.100e+01, 2.400e+01, 1.400e+01, 3.100e+01, 2.900e+01, 2.800e+01,
2.400e+01, 2.400e+01, 4.000e+01, 2.600e+01, 5.200e+01, 3.900e+01,
5.700e+01, 4.600e+01, 8.400e+01, 7.600e+01, 8.900e+01, 8.000e+01,
1.060e+02, 1.130e+02, 1.120e+02, 9.000e+01, 1.160e+02, 1.090e+02,
1.270e+02, 1.350e+02, 9.800e+01, 1.310e+02, 1.230e+02, 1.110e+02,
1.230e+02, 1.160e+02, 1.010e+02, 1.170e+02, 1.000e+02, 1.010e+02,
9.000e+01, 1.060e+02, 1.260e+02, 1.040e+02, 1.070e+02, 1.110e+02,
1.380e+02, 1.000e+02, 1.340e+02, 1.210e+02, 1.400e+02, 1.320e+02,
1.390e+02, 1.160e+02, 1.330e+02, 1.180e+02, 1.080e+02, 1.170e+02,
1.280e+02, 1.200e+02, 1.210e+02, 1.100e+02, 1.160e+02, 1.180e+02,
9.700e+01, 9.700e+01, 1.140e+02, 1.070e+02, 1.170e+02, 8.700e+01,
1.070e+02, 9.800e+01, 1.040e+02, 1.120e+02, 1.110e+02, 1.180e+02,
1.240e+02, 1.340e+02, 1.200e+02, 1.410e+02, 1.520e+02, 1.360e+02,
1.610e+02, 1.380e+02, 1.620e+02, 1.570e+02, 1.350e+02, 1.470e+02,
1.690e+02, 1.710e+02, 1.820e+02, 1.980e+02, 1.970e+02, 2.060e+02,
2.160e+02, 2.460e+02, 2.210e+02, 2.520e+02, 2.890e+02, 3.450e+02,
3.620e+02, 3.760e+02, 4.480e+02, 4.630e+02, 5.170e+02, 6.000e+02,
6.200e+02, 6.410e+02, 7.440e+02, 7.120e+02, 8.330e+02, 9.290e+02,
1.061e+03, 1.280e+03, 1.340e+03, 1.638e+03, 1.740e+03, 1.953e+03,
2.151e+03, 2.290e+03, 2.440e+03, 2.758e+03, 2.896e+03, 3.384e+03,
4.332e+03, 5.584e+03, 6.197e+03, 6.422e+03, 6.404e+03, 7.181e+03,
8.196e+03, 7.968e+03, 7.474e+03, 7.926e+03, 8.460e+03, 8.091e+03,
9.148e+03, 8.563e+03, 6.747e+03, 6.074e+03, 6.328e+03, 5.291e+03,
6.472e+03, 6.268e+03, 2.864e+03, 3.760e+02, 1.620e+02, 1.180e+02,
1.270e+02, 9.500e+01, 7.600e+01, 8.200e+01, 6.200e+01, 6.700e+01,
5.600e+01, 5.900e+01, 4.000e+01, 4.200e+01, 3.000e+01, 3.400e+01,
3.200e+01, 4.300e+01, 4.200e+01, 2.300e+01, 2.800e+01, 1.900e+01,
2.200e+01, 1.600e+01, 1.200e+01, 1.800e+01, 9.000e+00, 1.000e+01,
1.700e+01, 5.000e+00, 2.100e+01, 1.300e+01, 8.000e+00, 1.200e+01,
1.000e+01, 8.000e+00, 8.000e+00, 5.000e+00, 1.300e+01, 6.000e+00,
3.000e+00, 7.000e+00, 6.000e+00, 2.000e+00, 1.000e+00, 5.000e+00,
3.000e+00, 3.000e+00, 1.000e+00, 1.000e+00, 1.000e+00, 5.000e+00,
0.000e+00, 1.000e+00, 3.000e+00, 0.000e+00, 1.000e+00, 1.000e+00,
2.000e+00, 1.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00,
0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00,
0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00,
0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00,
0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00,
0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00,
0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00]), array([0. , 0.00390625, 0.0078125 , 0.01171875, 0.015625 ,
0.01953125, 0.0234375 , 0.02734375, 0.03125 , 0.03515625,
0.0390625 , 0.04296875, 0.046875 , 0.05078125, 0.0546875 ,
0.05859375, 0.0625 , 0.06640625, 0.0703125 , 0.07421875,
0.078125 , 0.08203125, 0.0859375 , 0.08984375, 0.09375 ,
0.09765625, 0.1015625 , 0.10546875, 0.109375 , 0.11328125,
0.1171875 , 0.12109375, 0.125 , 0.12890625, 0.1328125 ,
0.13671875, 0.140625 , 0.14453125, 0.1484375 , 0.15234375,
0.15625 , 0.16015625, 0.1640625 , 0.16796875, 0.171875 ,
0.17578125, 0.1796875 , 0.18359375, 0.1875 , 0.19140625,
0.1953125 , 0.19921875, 0.203125 , 0.20703125, 0.2109375 ,
0.21484375, 0.21875 , 0.22265625, 0.2265625 , 0.23046875,
0.234375 , 0.23828125, 0.2421875 , 0.24609375, 0.25 ,
0.25390625, 0.2578125 , 0.26171875, 0.265625 , 0.26953125,
0.2734375 , 0.27734375, 0.28125 , 0.28515625, 0.2890625 ,
0.29296875, 0.296875 , 0.30078125, 0.3046875 , 0.30859375,
0.3125 , 0.31640625, 0.3203125 , 0.32421875, 0.328125 ,
0.33203125, 0.3359375 , 0.33984375, 0.34375 , 0.34765625,
0.3515625 , 0.35546875, 0.359375 , 0.36328125, 0.3671875 ,
0.37109375, 0.375 , 0.37890625, 0.3828125 , 0.38671875,
0.390625 , 0.39453125, 0.3984375 , 0.40234375, 0.40625 ,
0.41015625, 0.4140625 , 0.41796875, 0.421875 , 0.42578125,
0.4296875 , 0.43359375, 0.4375 , 0.44140625, 0.4453125 ,
0.44921875, 0.453125 , 0.45703125, 0.4609375 , 0.46484375,
0.46875 , 0.47265625, 0.4765625 , 0.48046875, 0.484375 ,
0.48828125, 0.4921875 , 0.49609375, 0.5 , 0.50390625,
0.5078125 , 0.51171875, 0.515625 , 0.51953125, 0.5234375 ,
0.52734375, 0.53125 , 0.53515625, 0.5390625 , 0.54296875,
0.546875 , 0.55078125, 0.5546875 , 0.55859375, 0.5625 ,
0.56640625, 0.5703125 , 0.57421875, 0.578125 , 0.58203125,
0.5859375 , 0.58984375, 0.59375 , 0.59765625, 0.6015625 ,
0.60546875, 0.609375 , 0.61328125, 0.6171875 , 0.62109375,
0.625 , 0.62890625, 0.6328125 , 0.63671875, 0.640625 ,
0.64453125, 0.6484375 , 0.65234375, 0.65625 , 0.66015625,
0.6640625 , 0.66796875, 0.671875 , 0.67578125, 0.6796875 ,
0.68359375, 0.6875 , 0.69140625, 0.6953125 , 0.69921875,
0.703125 , 0.70703125, 0.7109375 , 0.71484375, 0.71875 ,
0.72265625, 0.7265625 , 0.73046875, 0.734375 , 0.73828125,
0.7421875 , 0.74609375, 0.75 , 0.75390625, 0.7578125 ,
0.76171875, 0.765625 , 0.76953125, 0.7734375 , 0.77734375,
0.78125 , 0.78515625, 0.7890625 , 0.79296875, 0.796875 ,
0.80078125, 0.8046875 , 0.80859375, 0.8125 , 0.81640625,
0.8203125 , 0.82421875, 0.828125 , 0.83203125, 0.8359375 ,
0.83984375, 0.84375 , 0.84765625, 0.8515625 , 0.85546875,
0.859375 , 0.86328125, 0.8671875 , 0.87109375, 0.875 ,
0.87890625, 0.8828125 , 0.88671875, 0.890625 , 0.89453125,
0.8984375 , 0.90234375, 0.90625 , 0.91015625, 0.9140625 ,
0.91796875, 0.921875 , 0.92578125, 0.9296875 , 0.93359375,
0.9375 , 0.94140625, 0.9453125 , 0.94921875, 0.953125 ,
0.95703125, 0.9609375 , 0.96484375, 0.96875 , 0.97265625,
0.9765625 , 0.98046875, 0.984375 , 0.98828125, 0.9921875 ,
0.99609375, 1. ]), <BarContainer object of 256 artists>)
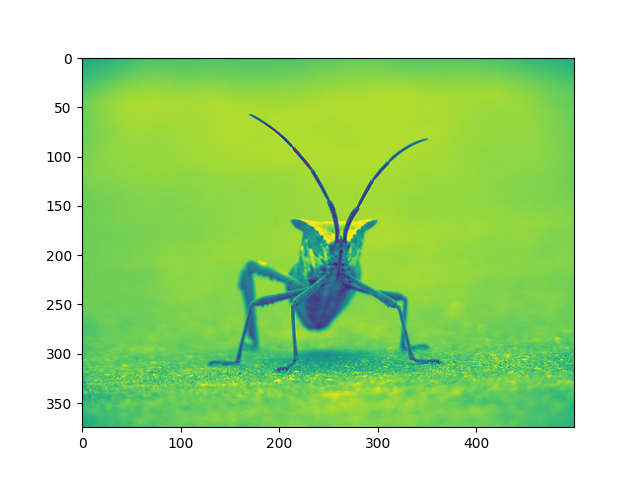
Nel nostro istogramma, sembra che non ci siano molte informazioni utili nella fascia alta (non molte cose bianche nell'immagine). Regoviamo il limite superiore, in modo che "ingrandiamo efficacemente" la parte dell'istogramma. Lo facciamo passando l'argomento in clima a Imshow.
set_clim()
È possibile specificare la clima nella chiamata plot.
imgplot = plt.imshow(lum_img, clim=(0.0, 0.7))
È inoltre possibile specificare la clima usando l'oggetto restituito
fig = plt.figure()
ax = fig.add_subplot(1, 2, 1)
imgplot = plt.imshow(lum_img)
ax.set_title('Before')
plt.colorbar(ticks=[0.1, 0.3, 0.5, 0.7], orientation='horizontal')
ax = fig.add_subplot(1, 2, 2)
imgplot = plt.imshow(lum_img)
imgplot.set_clim(0.0, 0.7)
ax.set_title('After')
plt.colorbar(ticks=[0.1, 0.3, 0.5, 0.7], orientation='horizontal')
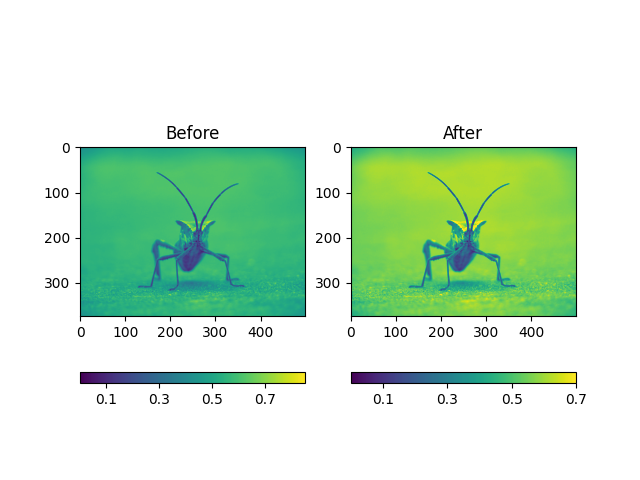
<matplotlib.colorbar.Colorbar object at 0x7f2cdf75fa30>
Schemi di interpolazione dell'array #
L'interpolazione calcola ciò che il colore o il valore di un pixel "dovrebbe" essere, secondo diversi schemi matematici. Un posto comune che ciò accade è quando si ridimensiona un'immagine. Il numero di pixel cambia, ma desideri le stesse informazioni. Poiché i pixel sono discreti, manca spazio. L'interpolazione è il modo in cui riempi quello spazio. Questo è il motivo per cui le tue immagini a volte escono sembrando pixelate quando le fate saltare in aria. L'effetto è più pronunciato quando la differenza tra l'immagine originale e l'immagine ampliata è maggiore. Prendiamo la nostra immagine e restringiamola. Stiamo effettivamente scartando i pixel, mantenendo solo pochi selezionati. Ora, quando lo tracciamo, quei dati vengono fatti esplodere fino alle dimensioni sullo schermo. I vecchi pixel non ci sono più e il computer deve disegnare pixel per riempire quello spazio.
Useremo la libreria Pillow che abbiamo usato per caricare l'immagine anche per ridimensionare l'immagine.
from PIL import Image
img = Image.open('../../doc/_static/stinkbug.png')
img.thumbnail((64, 64)) # resizes image in-place
imgplot = plt.imshow(img)
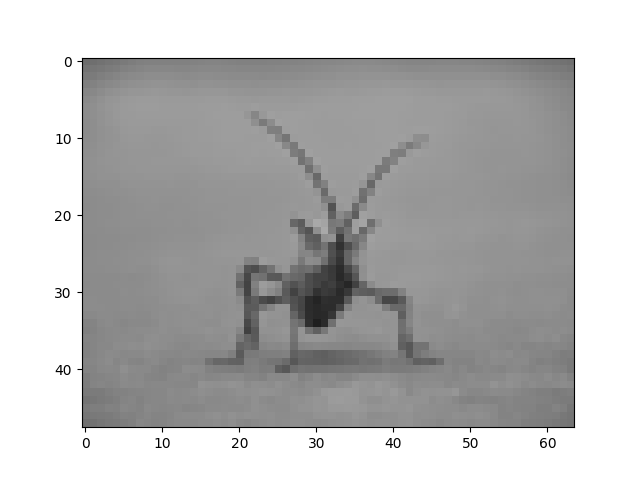
Qui abbiamo l'interpolazione predefinita, bilineare, poiché non abbiamo fornito imshow()alcun argomento di interpolazione.
Proviamo con altri. Ecco "più vicino", che non esegue alcuna interpolazione.
imgplot = plt.imshow(img, interpolation="nearest")
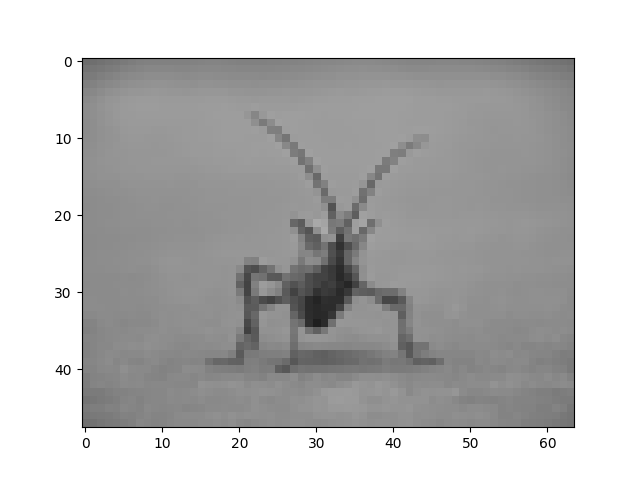
e bicubico:
imgplot = plt.imshow(img, interpolation="bicubic")
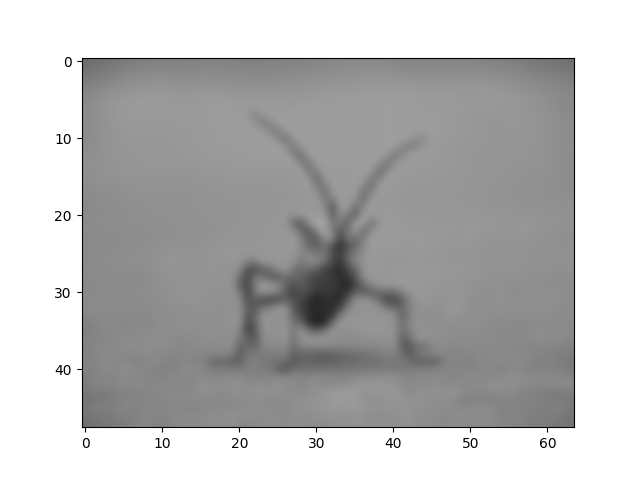
L'interpolazione bicubica viene spesso utilizzata quando si ingrandiscono le foto: le persone tendono a preferire sfocate piuttosto che pixelate.
Tempo di esecuzione totale dello script: (0 minuti 8,344 secondi)