Tutorial sulle trasformazioni

Come qualsiasi pacchetto grafico, Matplotlib è costruito su un framework di trasformazione per spostarsi facilmente tra i sistemi di coordinate, il sistema di coordinate dei dati userland, il sistema di coordinate degli assi , il sistema di coordinate della figura e il sistema di coordinate di visualizzazione . Nel 95% della tua trama, non avrai bisogno di pensarci, come succede sotto il cofano, ma mentre spingi i limiti della generazione di figure personalizzate, aiuta ad avere una comprensione di questi oggetti in modo da poter riutilizzare l'esistente trasformazioni che Matplotlib ti mette a disposizione, o crearne di tue (vedi matplotlib.transforms). La tabella seguente riassume alcuni sistemi di coordinate utili, una descrizione di ciascun sistema e l'oggetto di trasformazione per passare da ciascun sistema di coordinate alvisualizzare le coordinate. Nella colonna "Transformation Object", axè Axesun'istanza, figè Figureun'istanza ed subfigureè SubFigureun'istanza.

Sistema di coordinate	Descrizione	Oggetto di trasformazione da sistema a display
"dati"	Il sistema di coordinate dei dati in Axes.	ax.transData
"assi"	Il sistema di coordinate di Axes; (0, 0) è in basso a sinistra degli assi e (1, 1) è in alto a destra degli assi.	ax.transAxes
"sottofigura"	Il sistema di coordinate di SubFigure; (0, 0) è in basso a sinistra della sottofigura e (1, 1) è in alto a destra della sottofigura. Se una figura non ha sottofigure, è uguale a transFigure.	subfigure.transSubfigure
"figura"	Il sistema di coordinate di Figure; (0, 0) è in basso a sinistra della figura e (1, 1) è in alto a destra della figura.	fig.transFigure
"figura pollici"	Il sistema di coordinate Figurein pollici; (0, 0) è in basso a sinistra della figura e (larghezza, altezza) è in alto a destra della figura in pollici.	fig.dpi_scale_trans
"asse x", "asse y"	Sistemi di coordinate combinati, utilizzando le coordinate dei dati in una direzione e le coordinate degli assi nell'altra.	ax.get_xaxis_transform(), ax.get_yaxis_transform()
"Schermo"	Il sistema di coordinate nativo dell'output ; (0, 0) è la parte inferiore sinistra della finestra e (larghezza, altezza) è la parte superiore destra dell'output in "unità di visualizzazione". L'esatta interpretazione delle unità dipende dal back-end. Ad esempio, sono pixel per Agg e punti per svg/pdf.	None, o IdentityTransform()

Gli Transformoggetti sono ingenui rispetto ai sistemi di coordinate di origine e di destinazione, tuttavia gli oggetti a cui si fa riferimento nella tabella precedente sono costruiti per ricevere input nel proprio sistema di coordinate e trasformare l'input nel sistema di coordinate di visualizzazione . Questo è il motivo per cui il sistema di coordinate di visualizzazioneNone ha per la colonna "Oggetto di trasformazione" -- è già nelle coordinate di visualizzazione . Le convenzioni di denominazione e destinazione sono un aiuto per tenere traccia dei sistemi di coordinate e delle trasformazioni "standard" disponibili.

Le trasformazioni sanno anche come invertire se stesse (tramite Transform.inverted) per generare una trasformazione dal sistema di coordinate di output al sistema di coordinate di input. Ad esempio, ax.transDataconverte i valori nelle coordinate dei dati per visualizzare le coordinate ed ax.transData.inversed()è un matplotlib.transforms.Transformoggetto che va dalle coordinate di visualizzazione alle coordinate dei dati. Ciò è particolarmente utile quando si elaborano eventi dall'interfaccia utente, che in genere si verificano nello spazio di visualizzazione, e si desidera sapere dove si è verificato il clic del mouse o la pressione del tasto nel sistema di coordinate dei dati .

Si noti che specificando la posizione degli artisti nelle coordinate di visualizzazionedpi è possibile modificare la loro posizione relativa se la dimensione o la figura cambia. Ciò può causare confusione durante la stampa o la modifica della risoluzione dello schermo, poiché l'oggetto può cambiare posizione e dimensione. Pertanto è più comune per gli artisti collocati in un Axes o in una figura avere la loro trasformazione impostata su qualcosa di diverso da IdentityTransform(); l'impostazione predefinita quando un artista viene aggiunto a un Axes using add_artistè che la trasformazione sia ax.transDatatale da poter lavorare e pensare in coordinate di dati e lasciare che Matplotlib si occupi della trasformazione da visualizzare .

Coordinate dati

Cominciamo con la coordinata più comunemente usata, il sistema di coordinate dei dati . Ogni volta che aggiungi dati agli assi, Matplotlib aggiorna i datalimits, più comunemente aggiornati con i metodi set_xlim()e . set_ylim()Ad esempio, nella figura seguente, i limiti dei dati vanno da 0 a 10 sull'asse x e da -1 a 1 sull'asse y.

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches

x = np.arange(0, 10, 0.005)
y = np.exp(-x/2.) * np.sin(2*np.pi*x)

fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_xlim(0, 10)
ax.set_ylim(-1, 1)

plt.show()

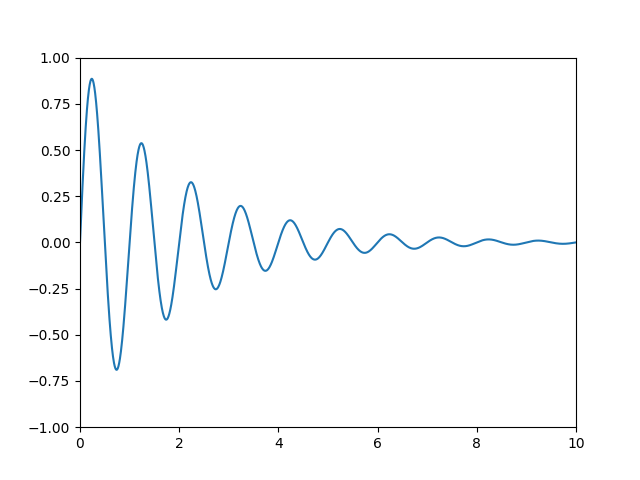
Puoi utilizzare l' ax.transDataistanza per trasformare i tuoi dati nel tuo sistema di coordinate di visualizzazione , un singolo punto o una sequenza di punti come mostrato di seguito:

In [14]: type(ax.transData)
Out[14]: <class 'matplotlib.transforms.CompositeGenericTransform'>

In [15]: ax.transData.transform((5, 0))
Out[15]: array([ 335.175,  247.   ])

In [16]: ax.transData.transform([(5, 0), (1, 2)])
Out[16]:
array([[ 335.175,  247.   ],
       [ 132.435,  642.2  ]])

Puoi utilizzare il inverted() metodo per creare una trasformazione che ti porterà dal display alle coordinate dei dati :

In [41]: inv = ax.transData.inverted()

In [42]: type(inv)
Out[42]: <class 'matplotlib.transforms.CompositeGenericTransform'>

In [43]: inv.transform((335.175,  247.))
Out[43]: array([ 5.,  0.])

Se stai digitando insieme a questo tutorial, i valori esatti delle coordinate di visualizzazione potrebbero differire se hai una dimensione della finestra o un'impostazione dpi diversa. Allo stesso modo, nella figura seguente, i punti etichettati visualizzati probabilmente non sono gli stessi della sessione ipython perché le dimensioni predefinite della figura della documentazione sono diverse.

x = np.arange(0, 10, 0.005)
y = np.exp(-x/2.) * np.sin(2*np.pi*x)

fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_xlim(0, 10)
ax.set_ylim(-1, 1)

xdata, ydata = 5, 0
# This computing the transform now, if anything
# (figure size, dpi, axes placement, data limits, scales..)
# changes re-calling transform will get a different value.
xdisplay, ydisplay = ax.transData.transform((xdata, ydata))

bbox = dict(boxstyle="round", fc="0.8")
arrowprops = dict(
    arrowstyle="->",
    connectionstyle="angle,angleA=0,angleB=90,rad=10")

offset = 72
ax.annotate('data = (%.1f, %.1f)' % (xdata, ydata),
            (xdata, ydata), xytext=(-2*offset, offset), textcoords='offset points',
            bbox=bbox, arrowprops=arrowprops)

disp = ax.annotate('display = (%.1f, %.1f)' % (xdisplay, ydisplay),
                   (xdisplay, ydisplay), xytext=(0.5*offset, -offset),
                   xycoords='figure pixels',
                   textcoords='offset points',
                   bbox=bbox, arrowprops=arrowprops)

plt.show()

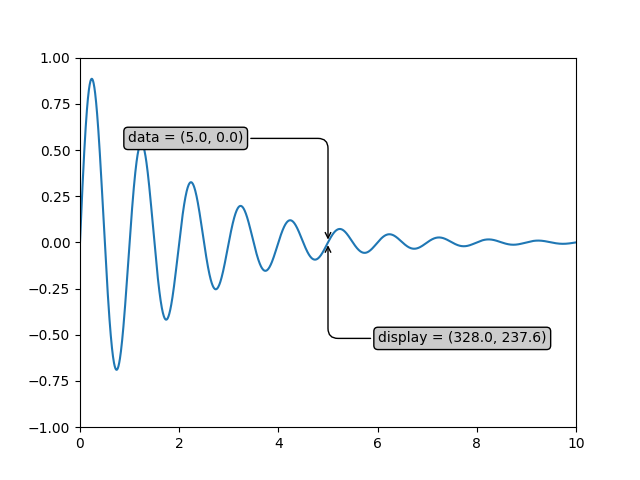
Avvertimento

Se esegui il codice sorgente nell'esempio sopra in un back-end GUI, potresti anche scoprire che le due frecce per i dati e le annotazioni di visualizzazione non puntano esattamente allo stesso punto. Questo perché il punto di visualizzazione è stato calcolato prima che la figura fosse visualizzata e il back-end della GUI potrebbe ridimensionare leggermente la figura quando viene creata. L'effetto è più pronunciato se ridimensioni tu stesso la figura. Questo è un buon motivo per cui raramente vuoi lavorare nello spazio di visualizzazione , ma puoi connetterti a 'on_draw' Eventper aggiornare le coordinate delle figure sui disegni delle figure; vedere Gestione e selezione degli eventi .

Quando modifichi i limiti x o y degli assi, i limiti dei dati vengono aggiornati in modo che la trasformazione produca un nuovo punto di visualizzazione. Si noti che quando cambiamo solo ylim, viene modificata solo la coordinata di visualizzazione y, e quando cambiamo anche xlim, vengono modificate entrambe. Ne parleremo più avanti quando parleremo di Bbox.

In [54]: ax.transData.transform((5, 0))
Out[54]: array([ 335.175,  247.   ])

In [55]: ax.set_ylim(-1, 2)
Out[55]: (-1, 2)

In [56]: ax.transData.transform((5, 0))
Out[56]: array([ 335.175     ,  181.13333333])

In [57]: ax.set_xlim(10, 20)
Out[57]: (10, 20)

In [58]: ax.transData.transform((5, 0))
Out[58]: array([-171.675     ,  181.13333333])

Coordinate assi

Dopo il sistema di coordinate dei dati , gli assi sono probabilmente il secondo sistema di coordinate più utile. Qui il punto (0, 0) è in basso a sinistra dei tuoi assi o sottotrama, (0.5, 0.5) è il centro e (1.0, 1.0) è in alto a destra. Puoi anche fare riferimento a punti al di fuori dell'intervallo, quindi (-0.1, 1.1) è a sinistra e sopra i tuoi assi. Questo sistema di coordinate è estremamente utile quando si inserisce il testo negli assi, perché spesso si desidera che una bolla di testo si trovi in ​​una posizione fissa, ad esempio, la parte superiore sinistra del riquadro degli assi, e che tale posizione rimanga fissa quando si esegue una panoramica o uno zoom. Ecco un semplice esempio che crea quattro pannelli e li etichetta 'A', 'B', 'C', 'D' come si vede spesso nei diari.

fig = plt.figure()
for i, label in enumerate(('A', 'B', 'C', 'D')):
    ax = fig.add_subplot(2, 2, i+1)
    ax.text(0.05, 0.95, label, transform=ax.transAxes,
            fontsize=16, fontweight='bold', va='top')

plt.show()

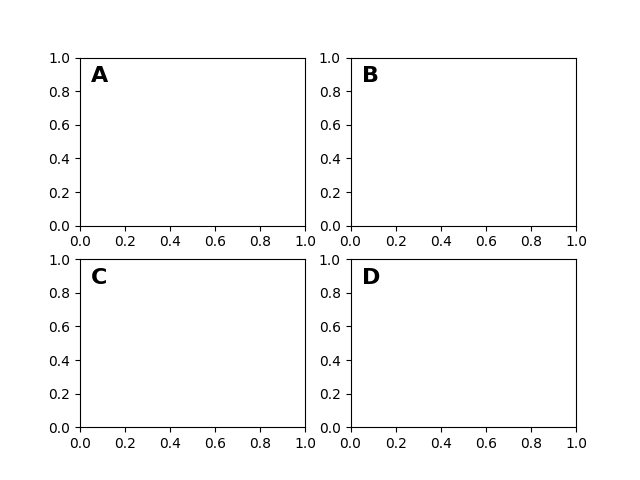
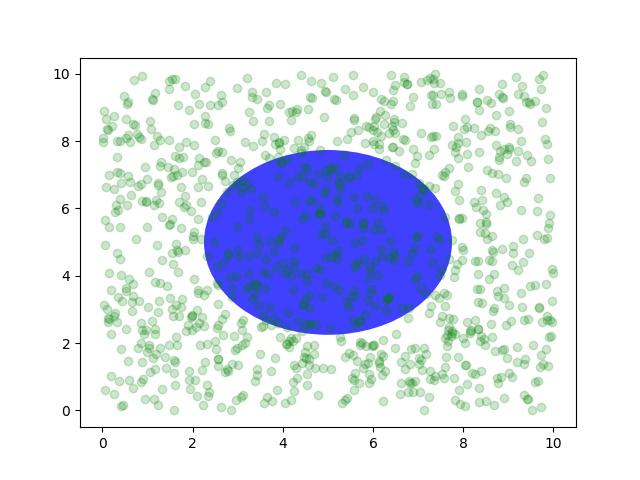
Puoi anche creare linee o patch nel sistema di coordinate degli assiax.transAxes , ma questo è meno utile nella mia esperienza rispetto all'utilizzo per posizionare il testo. Tuttavia, ecco un esempio sciocco che traccia alcuni punti casuali nello spazio dati e sovrappone un semitrasparente Circlecentrato nel mezzo degli assi con un raggio di un quarto degli assi - se i tuoi assi non mantengono le proporzioni (vedi set_aspect()) , sembrerà un'ellisse. Usa lo strumento pan/zoom per spostarti, o modifica manualmente i dati xlim e ylim, e vedrai i dati muoversi, ma il cerchio rimarrà fisso perché non è nelle coordinate dei dati e rimarrà sempre al centro degli assi .

fig, ax = plt.subplots()
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y, 'go', alpha=0.2)  # plot some data in data coordinates

circ = mpatches.Circle((0.5, 0.5), 0.25, transform=ax.transAxes,
                       facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()

Trasformazioni miste

Disegnare spazi di coordinate miste che mescolano assi con coordinate dati è estremamente utile, ad esempio per creare un'estensione orizzontale che evidenzi una regione dei dati y ma si estenda lungo l'asse x indipendentemente dai limiti dei dati, dal livello di panoramica o zoom, ecc. In effetti queste linee e campate unite sono così utili, abbiamo costruito delle funzioni per renderle facili da tracciare (vedi axhline(), axvline(), axhspan(), axvspan()) ma per scopi didattici implementeremo qui la campata orizzontale usando una trasformazione blended. Questo trucco funziona solo per trasformazioni separabili, come si vede nei normali sistemi di coordinate cartesiane, ma non per trasformazioni inseparabili come il PolarTransform.

import matplotlib.transforms as transforms

fig, ax = plt.subplots()
x = np.random.randn(1000)

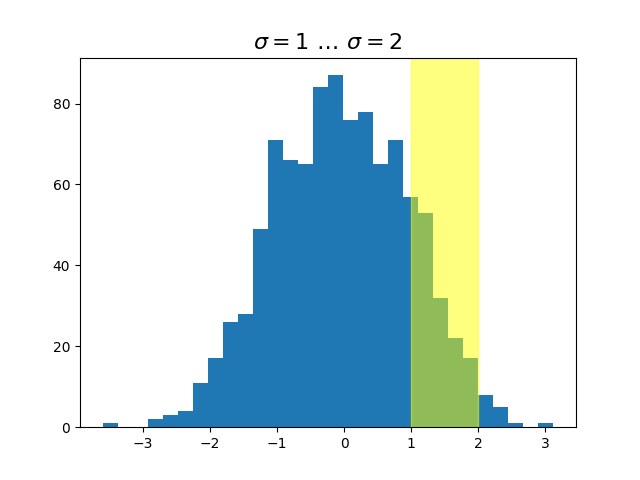
ax.hist(x, 30)
ax.set_title(r'$\sigma=1 \/ \dots \/ \sigma=2$', fontsize=16)

# the x coords of this transformation are data, and the y coord are axes
trans = transforms.blended_transform_factory(
    ax.transData, ax.transAxes)
# highlight the 1..2 stddev region with a span.
# We want x to be in data coordinates and y to span from 0..1 in axes coords.
rect = mpatches.Rectangle((1, 0), width=1, height=1, transform=trans,
                          color='yellow', alpha=0.5)
ax.add_patch(rect)

plt.show()

Nota

Le trasformazioni miste in cui x è nelle coordinate dei dati e y nelle coordinate degli assi è così utile che abbiamo metodi di supporto per restituire le versioni che Matplotlib usa internamente per disegnare segni di spunta, etichette di spunta, ecc. I metodi sono matplotlib.axes.Axes.get_xaxis_transform()e matplotlib.axes.Axes.get_yaxis_transform(). Quindi nell'esempio sopra, la chiamata a blended_transform_factory()può essere sostituita da get_xaxis_transform:

trans = ax.get_xaxis_transform()

Tracciare in coordinate fisiche

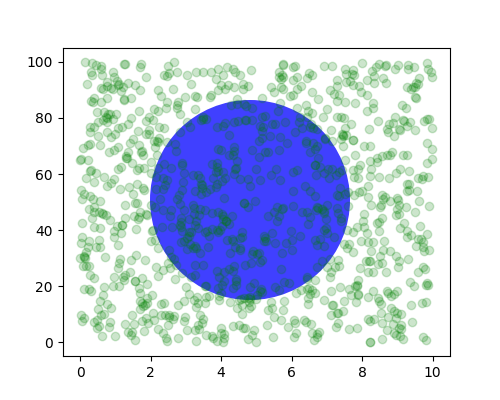
A volte vogliamo che un oggetto abbia una certa dimensione fisica sulla trama. Qui disegniamo lo stesso cerchio di cui sopra, ma in coordinate fisiche. Se fatto in modo interattivo, puoi vedere che la modifica della dimensione della figura non cambia l'offset del cerchio dall'angolo in basso a sinistra, non cambia la sua dimensione e il cerchio rimane un cerchio indipendentemente dalle proporzioni degli assi.

fig, ax = plt.subplots(figsize=(5, 4))
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y*10., 'go', alpha=0.2)  # plot some data in data coordinates
# add a circle in fixed-coordinates
circ = mpatches.Circle((2.5, 2), 1.0, transform=fig.dpi_scale_trans,
                       facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()

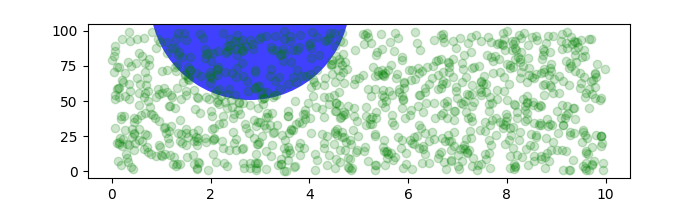
Se cambiamo la dimensione della figura, il cerchio non cambia la sua posizione assoluta e viene ritagliato.

fig, ax = plt.subplots(figsize=(7, 2))
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y*10., 'go', alpha=0.2)  # plot some data in data coordinates
# add a circle in fixed-coordinates
circ = mpatches.Circle((2.5, 2), 1.0, transform=fig.dpi_scale_trans,
                       facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()

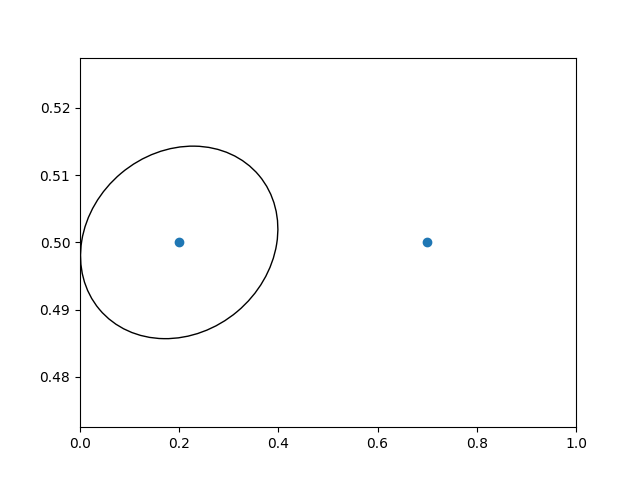
Un altro uso è mettere una patch con una dimensione fisica impostata attorno a un punto dati sugli assi. Qui aggiungiamo insieme due trasformazioni. Il primo imposta il ridimensionamento di quanto dovrebbe essere grande l'ellisse e il secondo ne imposta la posizione. L'ellisse viene quindi posizionata all'origine e quindi utilizziamo la trasformazione helper ScaledTranslation per spostarla nella posizione corretta nel ax.transDatasistema di coordinate. Questo helper è istanziato con:

trans = ScaledTranslation(xt, yt, scale_trans)

dove xt e yt sono gli offset di traduzione e scale_trans è una trasformazione che ridimensiona xt e yt al momento della trasformazione prima di applicare gli offset.

Si noti l'uso dell'operatore più sulle trasformazioni di seguito. Questo codice dice: prima applica la trasformazione della scala fig.dpi_scale_trans per rendere l'ellisse della dimensione corretta, ma ancora centrata su (0, 0), quindi traduci i dati in xdata[0]e ydata[0]nello spazio dati.

Nell'uso interattivo, l'ellisse rimane della stessa dimensione anche se i limiti degli assi vengono modificati tramite lo zoom.

fig, ax = plt.subplots()
xdata, ydata = (0.2, 0.7), (0.5, 0.5)
ax.plot(xdata, ydata, "o")
ax.set_xlim((0, 1))

trans = (fig.dpi_scale_trans +
         transforms.ScaledTranslation(xdata[0], ydata[0], ax.transData))

# plot an ellipse around the point that is 150 x 130 points in diameter...
circle = mpatches.Ellipse((0, 0), 150/72, 130/72, angle=40,
                          fill=None, transform=trans)
ax.add_patch(circle)
plt.show()

Nota

L'ordine di trasformazione è importante. Qui all'ellisse vengono prima assegnate le giuste dimensioni nello spazio di visualizzazione e poi spostate nello spazio dati nel punto corretto. Se avessimo fatto il ScaledTranslationprimo, allora xdata[0]e ydata[0]verrebbe prima trasformato per visualizzare le coordinate ( su un monitor a 200 dpi) e quindi quelle coordinate verrebbero ridimensionate spingendo il centro dell'ellisse ben fuori dallo schermo (cioè ).[ 358.4  475.2]fig.dpi_scale_trans[ 71680.  95040.]

Utilizzo delle trasformazioni offset per creare un effetto ombra

Un altro utilizzo di ScaledTranslationè creare una nuova trasformazione che sia sfalsata rispetto a un'altra trasformazione, ad esempio, per posizionare un oggetto leggermente spostato rispetto a un altro oggetto. In genere si desidera che lo spostamento avvenga in una dimensione fisica, come punti o pollici anziché nelle coordinate dei dati , in modo che l'effetto di spostamento sia costante a diversi livelli di zoom e impostazioni dpi.

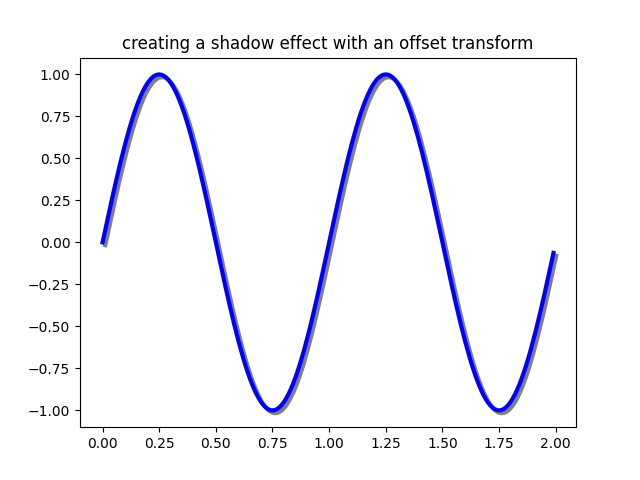
Un utilizzo per un offset è creare un effetto ombra, in cui si disegna un oggetto identico al primo appena a destra di esso, e appena sotto di esso, regolando lo zorder per assicurarsi che venga disegnata prima l'ombra e poi l'oggetto che è ombra sopra di esso.

Qui applichiamo le trasformazioni nell'ordine opposto all'uso di ScaledTranslationsopra. La trama viene prima creata in coordinate dati ( ax.transData) e quindi spostata di dxe dypunti utilizzando fig.dpi_scale_trans. (In tipografia, un punto è 1/72 pollici e, specificando i tuoi offset in punti, la tua figura avrà lo stesso aspetto indipendentemente dalla risoluzione dpi in cui è salvata.)

fig, ax = plt.subplots()

# make a simple sine wave
x = np.arange(0., 2., 0.01)
y = np.sin(2*np.pi*x)
line, = ax.plot(x, y, lw=3, color='blue')

# shift the object over 2 points, and down 2 points
dx, dy = 2/72., -2/72.
offset = transforms.ScaledTranslation(dx, dy, fig.dpi_scale_trans)
shadow_transform = ax.transData + offset

# now plot the same data with our offset transform;
# use the zorder to make sure we are below the line
ax.plot(x, y, lw=3, color='gray',
        transform=shadow_transform,
        zorder=0.5*line.get_zorder())

ax.set_title('creating a shadow effect with an offset transform')
plt.show()

Nota

L'offset dpi e pollici è un caso d'uso abbastanza comune che abbiamo una funzione di supporto speciale per crearlo in matplotlib.transforms.offset_copy(), che restituisce una nuova trasformazione con un offset aggiunto. Quindi sopra avremmo potuto fare:

shadow_transform = transforms.offset_copy(ax.transData,
         fig=fig, dx, dy, units='inches')

La pipeline di trasformazione

La ax.transDatatrasformazione con cui abbiamo lavorato in questo tutorial è un composto di tre diverse trasformazioni che comprendono la pipeline di trasformazione da dati -> visualizzazione coordinate. Michael Droettboom ha implementato il framework delle trasformazioni, avendo cura di fornire un'API pulita che separasse le proiezioni e le scale non lineari che si verificano nei grafici polari e logaritmici, dalle trasformazioni affini lineari che si verificano quando si esegue la panoramica e lo zoom. C'è un'efficienza qui, perché puoi eseguire una panoramica e ingrandire i tuoi assi che influiscono sulla trasformazione affine, ma potresti non aver bisogno di calcolare scale o proiezioni non lineari potenzialmente costose su semplici eventi di navigazione. È anche possibile moltiplicare insieme le matrici di trasformazione affine e quindi applicarle alle coordinate in un unico passaggio. Questo non è vero per tutte le possibili trasformazioni.

Ecco come ax.transDataviene definita l'istanza nella classe dell'asse separabile di base Axes:

self.transData = self.transScale + (self.transLimits + self.transAxes)

Siamo stati introdotti transAxesall'istanza sopra in Axes coordinates , che mappa gli angoli (0, 0), (1, 1) degli assi o il riquadro di delimitazione della sottotrama per visualizzare lo spazio, quindi diamo un'occhiata a questi altri due pezzi.

self.transLimitsè la trasformazione che ti porta dai dati alle coordinate degli assi ; cioè, mappa la tua vista xlim e ylim allo spazio unitario degli assi (e transAxesquindi prende quello spazio unitario per visualizzare lo spazio). Possiamo vederlo in azione qui

In [80]: ax = plt.subplot()

In [81]: ax.set_xlim(0, 10)
Out[81]: (0, 10)

In [82]: ax.set_ylim(-1, 1)
Out[82]: (-1, 1)

In [84]: ax.transLimits.transform((0, -1))
Out[84]: array([ 0.,  0.])

In [85]: ax.transLimits.transform((10, -1))
Out[85]: array([ 1.,  0.])

In [86]: ax.transLimits.transform((10, 1))
Out[86]: array([ 1.,  1.])

In [87]: ax.transLimits.transform((5, 0))
Out[87]: array([ 0.5,  0.5])

e possiamo usare questa stessa trasformazione invertita per tornare dalle coordinate degli assi delle unità alle coordinate dei dati .

In [90]: inv.transform((0.25, 0.25))
Out[90]: array([ 2.5, -0.5])

Il pezzo finale è l' self.transScaleattributo, che è responsabile della scala non lineare facoltativa dei dati, ad esempio per gli assi logaritmici. Quando un Axes è inizialmente impostato, questo è semplicemente impostato sulla trasformazione dell'identità, poiché gli assi Matplotlib di base hanno una scala lineare, ma quando chiami una funzione di ridimensionamento logaritmico come semilogx()o imposti esplicitamente la scala su logaritmica con set_xscale(), quindi l' ax.transScaleattributo è impostato per gestire la proiezione non lineare. Le scale trasformate sono proprietà delle rispettive xaxise yaxis Axisistanze. Ad esempio, quando chiami ax.set_xscale('log'), xaxis aggiorna la sua scala a matplotlib.scale.LogScaleun'istanza.

Per gli assi non separabili PolarAxes, c'è un altro pezzo da considerare, la trasformazione della proiezione. È transData matplotlib.projections.polar.PolarAxessimile a quello per i tipici assi matplotlib separabili, con un pezzo aggiuntivo transProjection:

self.transData = self.transScale + self.transProjection + \
    (self.transProjectionAffine + self.transAxes)

transProjectiongestisce la proiezione dallo spazio, ad esempio latitudine e longitudine per i dati cartografici, o raggio e theta per i dati polari, a un sistema di coordinate cartesiane separabile. Ci sono diversi esempi di proiezione nel matplotlib.projectionspacchetto e il modo migliore per saperne di più è aprire il sorgente per quei pacchetti e vedere come crearne uno tuo, poiché Matplotlib supporta assi e proiezioni estensibili. Michael Droettboom ha fornito un bell'esempio tutorial sulla creazione di assi di proiezione Hammer; vedere Proiezione personalizzata .