Normalizzazione della mappa dei colori

Gli oggetti che utilizzano le mappe dei colori per impostazione predefinita mappano linearmente i colori nella mappa dei colori dai valori dei dati vmin a vmax . Per esempio:

pcm = ax.pcolormesh(x, y, Z, vmin=-1., vmax=1., cmap='RdBu_r')

mapperà i dati in Z linearmente da -1 a +1, quindi Z=0 darà un colore al centro della colormap RdBu_r (bianco in questo caso).

Matplotlib esegue questa mappatura in due passaggi, con una normalizzazione dai dati di input a [0, 1] che si verifica prima e quindi la mappatura sugli indici nella mappa dei colori. Le normalizzazioni sono classi definite nel matplotlib.colors()modulo. La normalizzazione lineare predefinita è matplotlib.colors.Normalize().

Gli artisti che associano i dati al colore passano gli argomenti vmin e vmax per costruire matplotlib.colors.Normalize()un'istanza, quindi la chiamano:

In [1]: import matplotlib as mpl

In [2]: norm = mpl.colors.Normalize(vmin=-1, vmax=1)

In [3]: norm(0)
Out[3]: 0.5

Tuttavia, a volte ci sono casi in cui è utile mappare i dati alle mappe di colori in modo non lineare.

Logaritmico

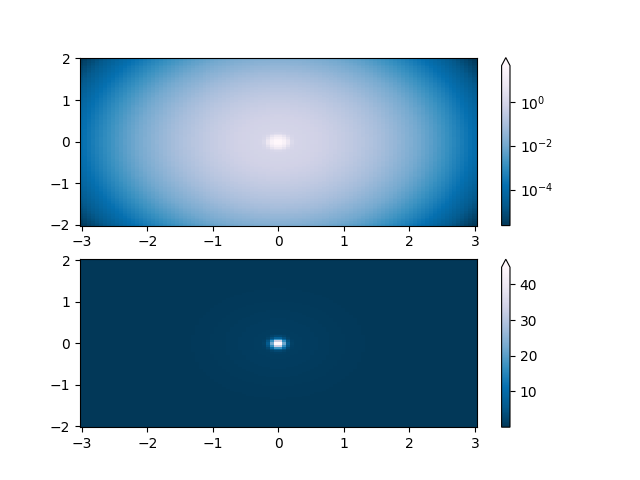
Una delle trasformazioni più comuni consiste nel tracciare i dati prendendo il suo logaritmo (in base 10). Questa trasformazione è utile per visualizzare le modifiche su scale diverse. L'utilizzo colors.LogNormnormalizza i dati tramite \(log_{10}\). Nell'esempio seguente, ci sono due protuberanze, una molto più piccola dell'altra. Utilizzando colors.LogNorm, è possibile vedere chiaramente la forma e la posizione di ciascuna protuberanza:

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import matplotlib.cbook as cbook
from matplotlib import cm

N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]

# A low hump with a spike coming out of the top right.  Needs to have
# z/colour axis on a log scale so we see both hump and spike.  linear
# scale only shows the spike.
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X * 10)**2 - (Y * 10)**2)
Z = Z1 + 50 * Z2

fig, ax = plt.subplots(2, 1)

pcm = ax[0].pcolor(X, Y, Z,
                   norm=colors.LogNorm(vmin=Z.min(), vmax=Z.max()),
                   cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='max')

pcm = ax[1].pcolor(X, Y, Z, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='max')
plt.show()

Centrato

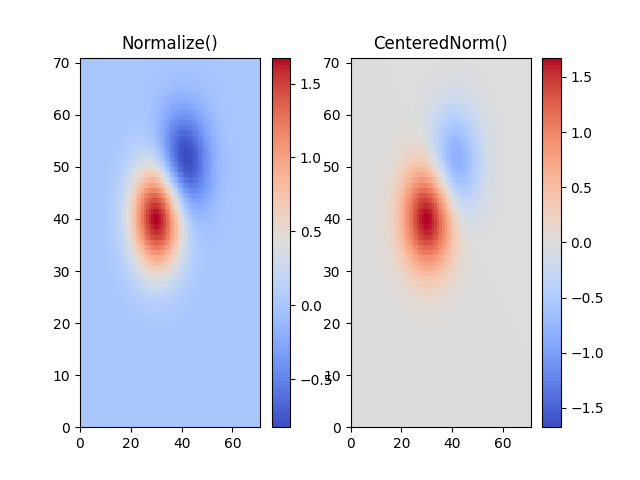
In molti casi, i dati sono simmetrici attorno a un centro, ad esempio anomalie positive e negative attorno a un centro 0. In questo caso, vorremmo mappare il centro a 0,5 e mappare il punto dati con la deviazione maggiore dal centro a 1.0, se il suo valore è maggiore del centro, o 0.0 in caso contrario. La norma colors.CenteredNormcrea tale mappatura automaticamente. È adatto per essere combinato con una mappa di colori divergente che utilizza bordi di colori diversi che si incontrano al centro in un colore insaturo.

Se il centro di simmetria è diverso da 0, può essere impostato con l' argomento vcenter . Per il ridimensionamento logaritmico su entrambi i lati del centro, vedi colors.SymLogNormsotto; per applicare una mappatura diversa sopra e sotto il centro, utilizzare colors.TwoSlopeNormbelow.

delta = 0.1
x = np.arange(-3.0, 4.001, delta)
y = np.arange(-4.0, 3.001, delta)
X, Y = np.meshgrid(x, y)
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (0.9*Z1 - 0.5*Z2) * 2

# select a divergent colormap
cmap = cm.coolwarm

fig, (ax1, ax2) = plt.subplots(ncols=2)
pc = ax1.pcolormesh(Z, cmap=cmap)
fig.colorbar(pc, ax=ax1)
ax1.set_title('Normalize()')

pc = ax2.pcolormesh(Z, norm=colors.CenteredNorm(), cmap=cmap)
fig.colorbar(pc, ax=ax2)
ax2.set_title('CenteredNorm()')

plt.show()

Logaritmico simmetrico

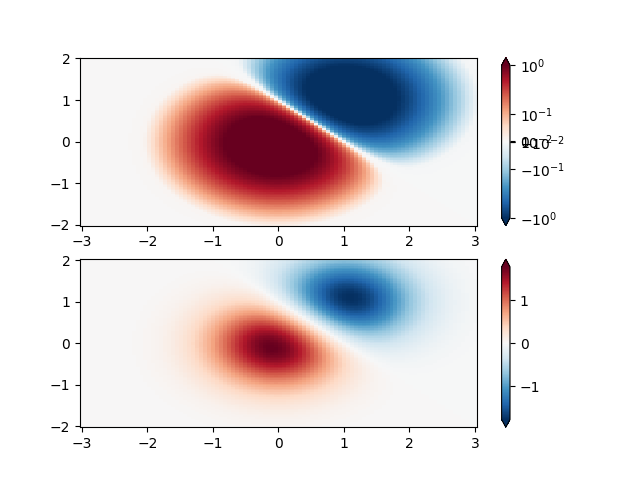
Allo stesso modo, a volte capita che ci siano dati positivi e negativi, ma vorremmo comunque applicare un ridimensionamento logaritmico ad entrambi. In questo caso, i numeri negativi sono anche ridimensionati logaritmicamente e mappati su numeri più piccoli; ad esempio, se vmin=-vmax, i numeri negativi vengono mappati da 0 a 0,5 e quelli positivi da 0,5 a 1.

Poiché il logaritmo dei valori vicini allo zero tende all'infinito, è necessario mappare linearmente un piccolo intervallo intorno allo zero. Il parametro Lindresh consente all'utente di specificare la dimensione di questo intervallo (- Lindresh , Lindresh ). La dimensione di questo intervallo nella mappa dei colori è impostata da linscale . Quando linscale == 1.0 (impostazione predefinita), lo spazio utilizzato per le metà positive e negative dell'intervallo lineare sarà uguale a una decade nell'intervallo logaritmico.

N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (Z1 - Z2) * 2

fig, ax = plt.subplots(2, 1)

pcm = ax[0].pcolormesh(X, Y, Z,
                       norm=colors.SymLogNorm(linthresh=0.03, linscale=0.03,
                                              vmin=-1.0, vmax=1.0, base=10),
                       cmap='RdBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='both')

pcm = ax[1].pcolormesh(X, Y, Z, cmap='RdBu_r', vmin=-np.max(Z), shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='both')
plt.show()

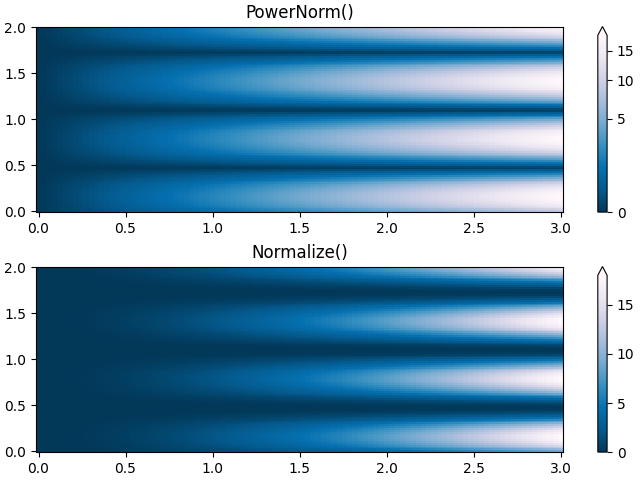
Legge di potenza

A volte è utile rimappare i colori su una relazione di legge di potere (es\(y=x^{\gamma}\), dove\(\gamma\)è il potere). Per questo usiamo il colors.PowerNorm. Ci vuole come argomento gamma ( gamma == 1.0 produrrà solo la normalizzazione lineare predefinita):

Nota

Probabilmente dovrebbe esserci una buona ragione per tracciare i dati utilizzando questo tipo di trasformazione. Gli spettatori tecnici vengono utilizzati per assi lineari e logaritmici e trasformazioni di dati. Le leggi sul potere sono meno comuni e gli spettatori dovrebbero essere esplicitamente informati di essere stati utilizzati.

N = 100
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2

fig, ax = plt.subplots(2, 1, constrained_layout=True)

pcm = ax[0].pcolormesh(X, Y, Z1, norm=colors.PowerNorm(gamma=0.5),
                       cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='max')
ax[0].set_title('PowerNorm()')

pcm = ax[1].pcolormesh(X, Y, Z1, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='max')
ax[1].set_title('Normalize()')
plt.show()

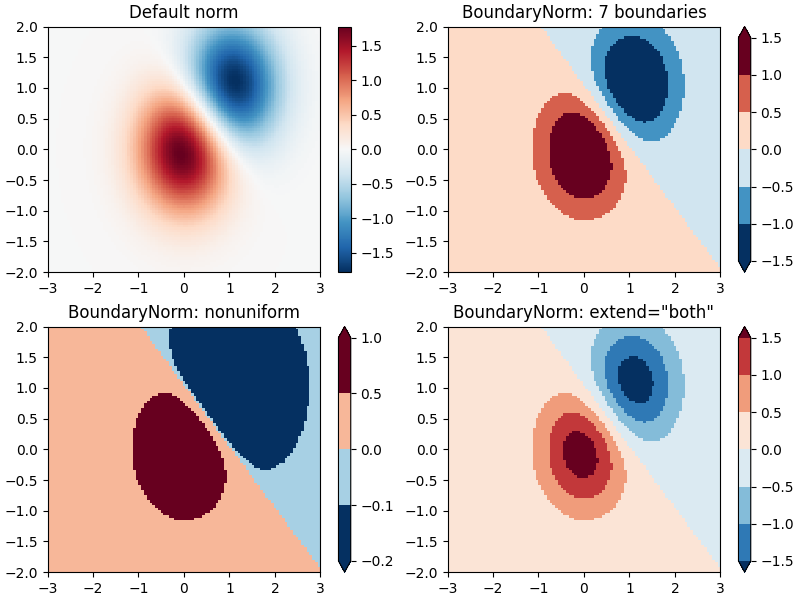
Limiti discreti

Un'altra normalizzazione fornita con Matplotlib è colors.BoundaryNorm. Oltre a vmin e vmax , questo accetta come argomenti i confini tra i quali i dati devono essere mappati. I colori vengono quindi distribuiti linearmente tra questi "limiti". Può anche utilizzare un argomento extend per aggiungere valori fuori limite superiore e/o inferiore all'intervallo su cui sono distribuiti i colori. Per esempio:

In [4]: import matplotlib.colors as colors

In [5]: bounds = np.array([-0.25, -0.125, 0, 0.5, 1])

In [6]: norm = colors.BoundaryNorm(boundaries=bounds, ncolors=4)

In [7]: print(norm([-0.2, -0.15, -0.02, 0.3, 0.8, 0.99]))
[0 0 1 2 3 3]

Nota: a differenza delle altre norme, questa norma restituisce valori da 0 a ncolors -1.

N = 100
X, Y = np.meshgrid(np.linspace(-3, 3, N), np.linspace(-2, 2, N))
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = ((Z1 - Z2) * 2)[:-1, :-1]

fig, ax = plt.subplots(2, 2, figsize=(8, 6), constrained_layout=True)
ax = ax.flatten()

# Default norm:
pcm = ax[0].pcolormesh(X, Y, Z, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[0], orientation='vertical')
ax[0].set_title('Default norm')

# Even bounds give a contour-like effect:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[1].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[1], extend='both', orientation='vertical')
ax[1].set_title('BoundaryNorm: 7 boundaries')

# Bounds may be unevenly spaced:
bounds = np.array([-0.2, -0.1, 0, 0.5, 1])
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[2].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[2], extend='both', orientation='vertical')
ax[2].set_title('BoundaryNorm: nonuniform')

# With out-of-bounds colors:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256, extend='both')
pcm = ax[3].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
# The colorbar inherits the "extend" argument from BoundaryNorm.
fig.colorbar(pcm, ax=ax[3], orientation='vertical')
ax[3].set_title('BoundaryNorm: extend="both"')
plt.show()

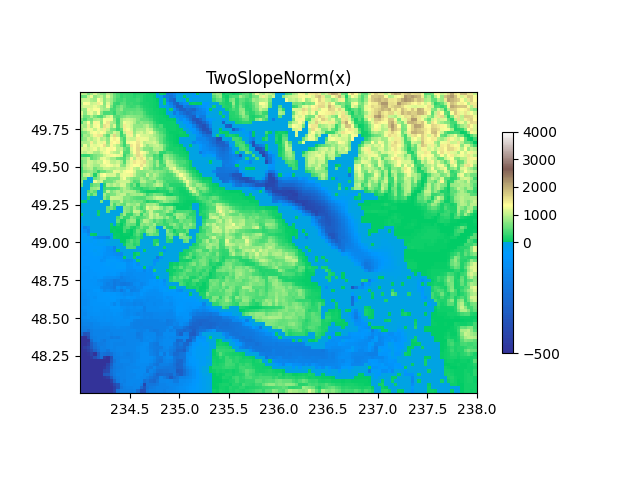
TwoSlopeNorm: mappatura diversa su entrambi i lati di un centro

A volte vogliamo avere una mappa di colori diversa su entrambi i lati di un punto centrale concettuale e vogliamo che queste due mappe di colori abbiano scale lineari diverse. Un esempio è una mappa topografica in cui la terra e l'oceano hanno un centro a zero, ma la terra ha tipicamente un intervallo di elevazione maggiore rispetto all'acqua ha un intervallo di profondità e sono spesso rappresentate da una mappa di colori diversa.

dem = cbook.get_sample_data('topobathy.npz', np_load=True)
topo = dem['topo']
longitude = dem['longitude']
latitude = dem['latitude']

fig, ax = plt.subplots()
# make a colormap that has land and ocean clearly delineated and of the
# same length (256 + 256)
colors_undersea = plt.cm.terrain(np.linspace(0, 0.17, 256))
colors_land = plt.cm.terrain(np.linspace(0.25, 1, 256))
all_colors = np.vstack((colors_undersea, colors_land))
terrain_map = colors.LinearSegmentedColormap.from_list(
    'terrain_map', all_colors)

# make the norm:  Note the center is offset so that the land has more
# dynamic range:
divnorm = colors.TwoSlopeNorm(vmin=-500., vcenter=0, vmax=4000)

pcm = ax.pcolormesh(longitude, latitude, topo, rasterized=True, norm=divnorm,
                    cmap=terrain_map, shading='auto')
# Simple geographic plot, set aspect ratio because distance between lines of
# longitude depends on latitude.
ax.set_aspect(1 / np.cos(np.deg2rad(49)))
ax.set_title('TwoSlopeNorm(x)')
cb = fig.colorbar(pcm, shrink=0.6)
cb.set_ticks([-500, 0, 1000, 2000, 3000, 4000])
plt.show()

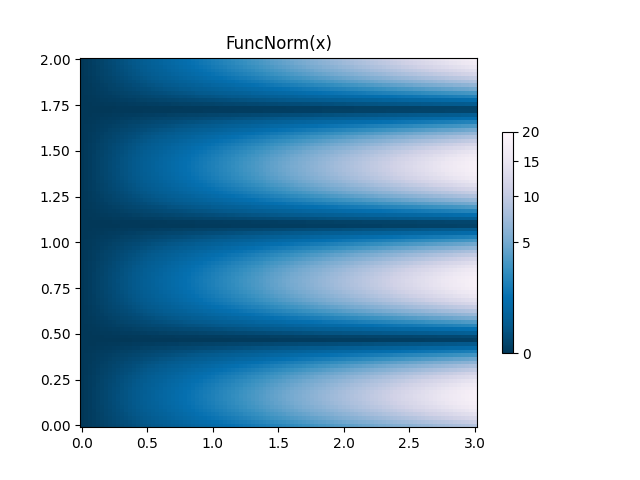
FuncNorm: normalizzazione della funzione arbitraria

Se le norme di cui sopra non forniscono la normalizzazione desiderata, è possibile utilizzarle FuncNormper definirne una propria. Si noti che questo esempio è lo stesso PowerNormdi una potenza di 0,5:

def _forward(x):
    return np.sqrt(x)


def _inverse(x):
    return x**2

N = 100
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2
fig, ax = plt.subplots()

norm = colors.FuncNorm((_forward, _inverse), vmin=0, vmax=20)
pcm = ax.pcolormesh(X, Y, Z1, norm=norm, cmap='PuBu_r', shading='auto')
ax.set_title('FuncNorm(x)')
fig.colorbar(pcm, shrink=0.6)
plt.show()

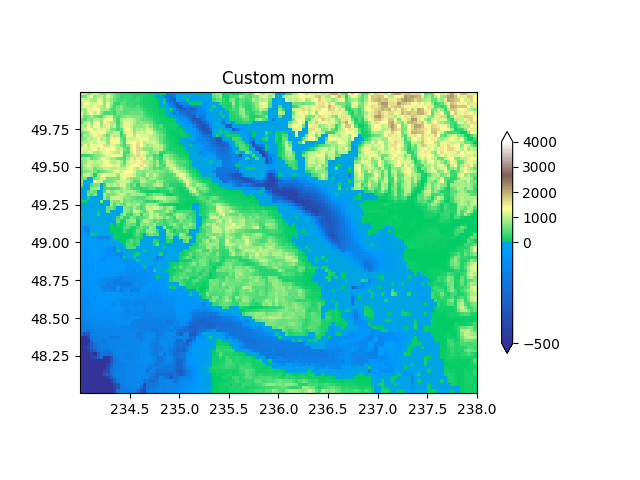
Normalizzazione personalizzata: implementa manualmente due intervalli lineari

Quanto TwoSlopeNormsopra descritto costituisce un utile esempio per definire la propria norma. Nota affinché la barra dei colori funzioni, devi definire un inverso per la tua norma:

class MidpointNormalize(colors.Normalize):
    def __init__(self, vmin=None, vmax=None, vcenter=None, clip=False):
        self.vcenter = vcenter
        super().__init__(vmin, vmax, clip)

    def __call__(self, value, clip=None):
        # I'm ignoring masked values and all kinds of edge cases to make a
        # simple example...
        # Note also that we must extrapolate beyond vmin/vmax
        x, y = [self.vmin, self.vcenter, self.vmax], [0, 0.5, 1.]
        return np.ma.masked_array(np.interp(value, x, y,
                                            left=-np.inf, right=np.inf))

    def inverse(self, value):
        y, x = [self.vmin, self.vcenter, self.vmax], [0, 0.5, 1]
        return np.interp(value, x, y, left=-np.inf, right=np.inf)


fig, ax = plt.subplots()
midnorm = MidpointNormalize(vmin=-500., vcenter=0, vmax=4000)

pcm = ax.pcolormesh(longitude, latitude, topo, rasterized=True, norm=midnorm,
                    cmap=terrain_map, shading='auto')
ax.set_aspect(1 / np.cos(np.deg2rad(49)))
ax.set_title('Custom norm')
cb = fig.colorbar(pcm, shrink=0.6, extend='both')
cb.set_ticks([-500, 0, 1000, 2000, 3000, 4000])

plt.show()