Tipi di proiezione della trama 3D

Dimostra le diverse proiezioni della telecamera per i grafici 3D e gli effetti della modifica della lunghezza focale per una proiezione prospettica. Si noti che Matplotlib corregge l'effetto "zoom" della modifica della lunghezza focale.

La lunghezza focale predefinita di 1 corrisponde a un campo visivo (FOV) di 90 gradi. Una lunghezza focale aumentata tra 1 e infinito "appiattisce" l'immagine, mentre una lunghezza focale ridotta tra 1 e 0 esagera la prospettiva e conferisce all'immagine una profondità più evidente. Nel caso limite, una lunghezza focale di infinito corrisponde a una proiezione ortografica dopo la correzione dell'effetto zoom.

Puoi calcolare la lunghezza focale da un FOV tramite l'equazione:

\[1 / \tan (\mathrm{FOV} / 2)\]

O vice versa:

\[\mathrm{FOV} = 2 \arctan (1 / \mathrm{focal length})\]

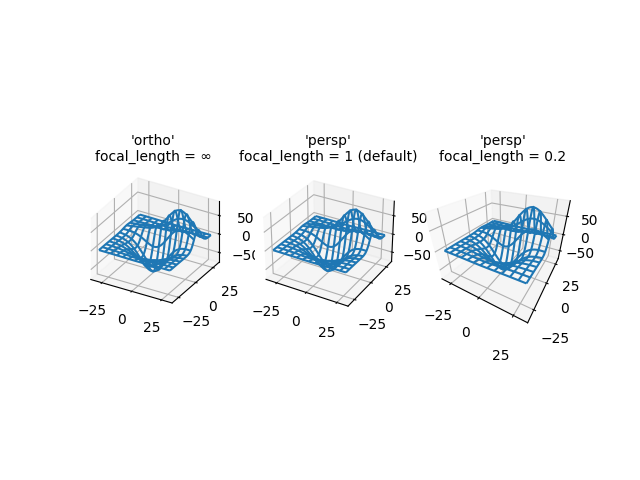
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt


fig, axs = plt.subplots(1, 3, subplot_kw={'projection': '3d'})

# Get the test data
X, Y, Z = axes3d.get_test_data(0.05)

# Plot the data
for ax in axs:
    ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)

# Set the orthographic projection.
axs[0].set_proj_type('ortho')  # FOV = 0 deg
axs[0].set_title("'ortho'\nfocal_length = ∞", fontsize=10)

# Set the perspective projections
axs[1].set_proj_type('persp')  # FOV = 90 deg
axs[1].set_title("'persp'\nfocal_length = 1 (default)", fontsize=10)

axs[2].set_proj_type('persp', focal_length=0.2)  # FOV = 157.4 deg
axs[2].set_title("'persp'\nfocal_length = 0.2", fontsize=10)

plt.show()