Riempi tra e Alpha

La fill_betweenfunzione genera una regione ombreggiata tra un limite minimo e massimo utile per illustrare gli intervalli. Ha un whereargomento molto utile per combinare il riempimento con intervalli logici, ad esempio, per riempire semplicemente una curva sopra un certo valore di soglia.

Al suo livello più elementare, fill_betweenpuò essere utilizzato per migliorare l'aspetto visivo di un grafico. Confrontiamo due grafici di dati finanziari con un semplice grafico a linee a sinistra e una linea piena a destra.

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.cbook as cbook


# load up some sample financial data
r = (cbook.get_sample_data('goog.npz', np_load=True)['price_data']
     .view(np.recarray))
# create two subplots with the shared x and y axes
fig, (ax1, ax2) = plt.subplots(1, 2, sharex=True, sharey=True)

pricemin = r.close.min()

ax1.plot(r.date, r.close, lw=2)
ax2.fill_between(r.date, pricemin, r.close, alpha=0.7)

for ax in ax1, ax2:
    ax.grid(True)
    ax.label_outer()

ax1.set_ylabel('price')

fig.suptitle('Google (GOOG) daily closing price')
fig.autofmt_xdate()

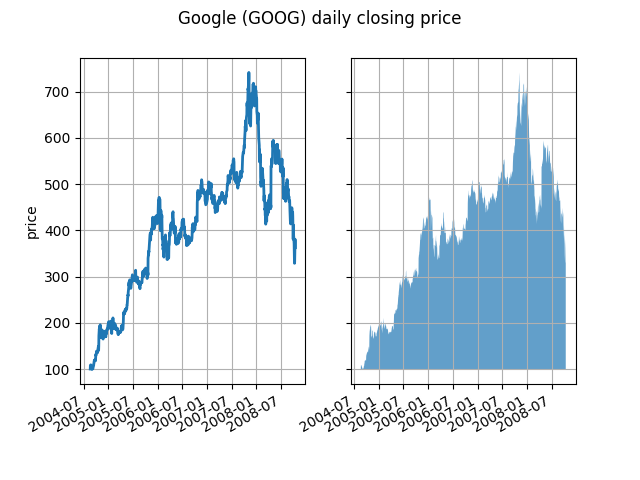
Il canale alfa non è necessario qui, ma può essere utilizzato per ammorbidire i colori per trame visivamente più accattivanti. In altri esempi, come vedremo di seguito, il canale alfa è funzionalmente utile in quanto le regioni ombreggiate possono sovrapporsi e l'alfa consente di vedere entrambi. Nota che il formato postscript non supporta alpha (questa è una limitazione postscript, non una limitazione matplotlib), quindi quando usi alpha salva le tue figure in PNG, PDF o SVG.

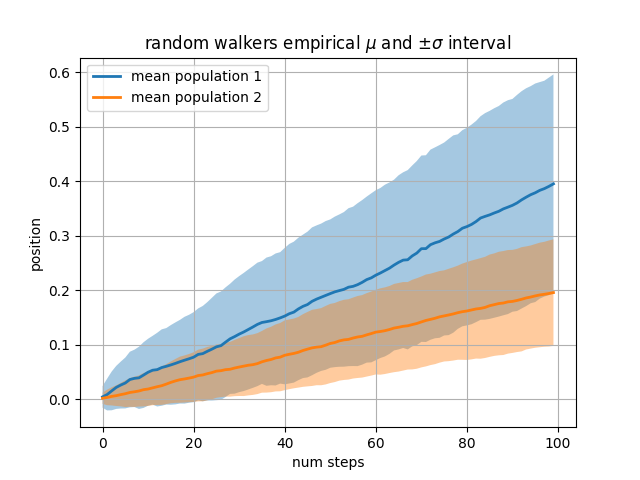
Il nostro prossimo esempio calcola due popolazioni di random walker con una diversa media e deviazione standard delle distribuzioni normali da cui sono tratti i passi. Usiamo le regioni piene per tracciare +/- una deviazione standard della posizione media della popolazione. Qui il canale alfa è utile, non solo estetico.

# Fixing random state for reproducibility
np.random.seed(19680801)

Nsteps, Nwalkers = 100, 250
t = np.arange(Nsteps)

# an (Nsteps x Nwalkers) array of random walk steps
S1 = 0.004 + 0.02*np.random.randn(Nsteps, Nwalkers)
S2 = 0.002 + 0.01*np.random.randn(Nsteps, Nwalkers)

# an (Nsteps x Nwalkers) array of random walker positions
X1 = S1.cumsum(axis=0)
X2 = S2.cumsum(axis=0)


# Nsteps length arrays empirical means and standard deviations of both
# populations over time
mu1 = X1.mean(axis=1)
sigma1 = X1.std(axis=1)
mu2 = X2.mean(axis=1)
sigma2 = X2.std(axis=1)

# plot it!
fig, ax = plt.subplots(1)
ax.plot(t, mu1, lw=2, label='mean population 1')
ax.plot(t, mu2, lw=2, label='mean population 2')
ax.fill_between(t, mu1+sigma1, mu1-sigma1, facecolor='C0', alpha=0.4)
ax.fill_between(t, mu2+sigma2, mu2-sigma2, facecolor='C1', alpha=0.4)
ax.set_title(r'random walkers empirical $\mu$ and $\pm \sigma$ interval')
ax.legend(loc='upper left')
ax.set_xlabel('num steps')
ax.set_ylabel('position')
ax.grid()

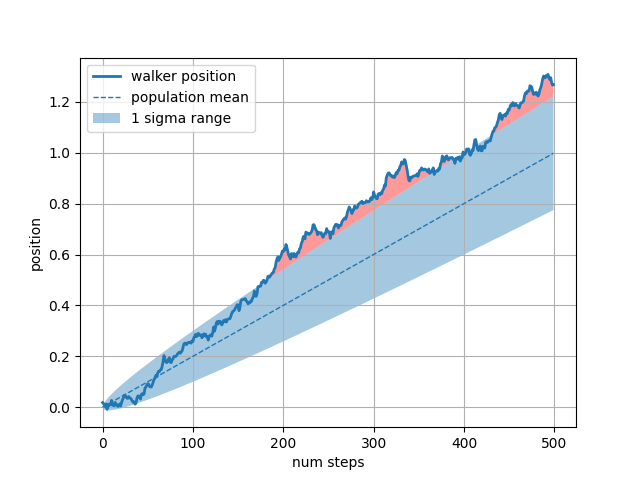
L' whereargomento della parola chiave è molto utile per evidenziare determinate aree del grafico. whereaccetta una maschera booleana della stessa lunghezza degli argomenti x, ymin e ymax e riempie solo la regione in cui la maschera booleana è True. Nell'esempio seguente, simuliamo un singolo random walker e calcoliamo la media analitica e la deviazione standard delle posizioni della popolazione. La media della popolazione è mostrata come linea tratteggiata e la deviazione più/meno un sigma dalla media è mostrata come regione piena. Usiamo la maschera where per trovare la regione in cui il deambulatore si trova al di fuori del confine di un sigma e ombreggiamo quella regione in rosso.X > upper_bound

# Fixing random state for reproducibility
np.random.seed(1)

Nsteps = 500
t = np.arange(Nsteps)

mu = 0.002
sigma = 0.01

# the steps and position
S = mu + sigma*np.random.randn(Nsteps)
X = S.cumsum()

# the 1 sigma upper and lower analytic population bounds
lower_bound = mu*t - sigma*np.sqrt(t)
upper_bound = mu*t + sigma*np.sqrt(t)

fig, ax = plt.subplots(1)
ax.plot(t, X, lw=2, label='walker position')
ax.plot(t, mu*t, lw=1, label='population mean', color='C0', ls='--')
ax.fill_between(t, lower_bound, upper_bound, facecolor='C0', alpha=0.4,
                label='1 sigma range')
ax.legend(loc='upper left')

# here we use the where argument to only fill the region where the
# walker is above the population 1 sigma boundary
ax.fill_between(t, upper_bound, X, where=X > upper_bound, fc='red', alpha=0.4)
ax.fill_between(t, lower_bound, X, where=X < lower_bound, fc='red', alpha=0.4)
ax.set_xlabel('num steps')
ax.set_ylabel('position')
ax.grid()

Un altro uso utile delle regioni piene è evidenziare le estensioni orizzontali o verticali di un asse, poiché Matplotlib ha le funzioni di supporto axhspane axvspan. Guarda la demo di axhspan .

plt.show()