Asinh Demo #

Illustrazione del asinhridimensionamento dell'asse, che utilizza la trasformazione

\[a \rightarrow a_0 \sinh^{-1} (a / a_0)\]

Per valori di coordinate vicini allo zero (cioè molto più piccoli della "larghezza lineare"\(a_0\)), ciò lascia sostanzialmente invariati i valori:

\[a \rightarrow a + \mathcal{O}(a^3)\]

ma per valori maggiori (es\(|a| \gg a_0\), questo è asintotico

\[a \rightarrow a_0 \, \mathrm{sgn}(a) \ln |a| + \mathcal{O}(1)\]

Come per lo symlogscaling, ciò consente di tracciare quantità che coprono un intervallo dinamico molto ampio che include sia valori positivi che negativi. Tuttavia, symlogcomporta una trasformazione che presenta discontinuità nel suo gradiente perché è costruita da trasformazioni lineari e logaritmiche separate . Il asinhridimensionamento utilizza una trasformazione uniforme per tutti i valori (finiti), che è matematicamente più pulita e riduce gli artefatti visivi associati a una brusca transizione tra le regioni lineari e logaritmiche del grafico.

Nota

scale.AsinhScaleè sperimentale e l'API potrebbe cambiare.

Vedi AsinhScale, SymmetricalLogScale.

import numpy as np
import matplotlib.pyplot as plt

# Prepare sample values for variations on y=x graph:
x = np.linspace(-3, 6, 500)

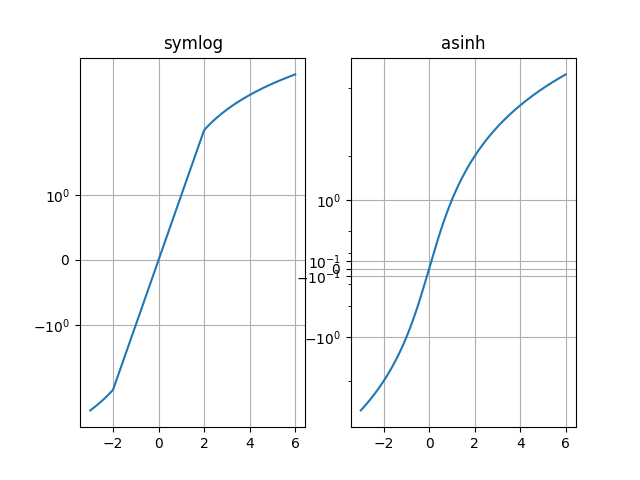
Confronta il comportamento di "symlog" e "asinh" sul grafico campione y=x, dove c'è un gradiente discontinuo in "symlog" vicino a y=2:

fig1 = plt.figure()
ax0, ax1 = fig1.subplots(1, 2, sharex=True)

ax0.plot(x, x)
ax0.set_yscale('symlog')
ax0.grid()
ax0.set_title('symlog')

ax1.plot(x, x)
ax1.set_yscale('asinh')
ax1.grid()
ax1.set_title('asinh')

Text(0.5, 1.0, 'asinh')

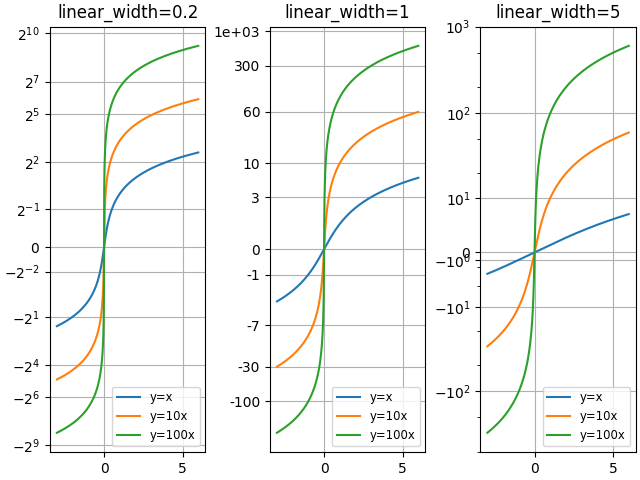
Confronta i grafici "asinh" con diversi parametri di scala "linear_width":

fig2 = plt.figure(constrained_layout=True)
axs = fig2.subplots(1, 3, sharex=True)
for ax, (a0, base) in zip(axs, ((0.2, 2), (1.0, 0), (5.0, 10))):
    ax.set_title('linear_width={:.3g}'.format(a0))
    ax.plot(x, x, label='y=x')
    ax.plot(x, 10*x, label='y=10x')
    ax.plot(x, 100*x, label='y=100x')
    ax.set_yscale('asinh', linear_width=a0, base=base)
    ax.grid()
    ax.legend(loc='best', fontsize='small')

linear_width=0.2, linear_width=1, linear_width=5

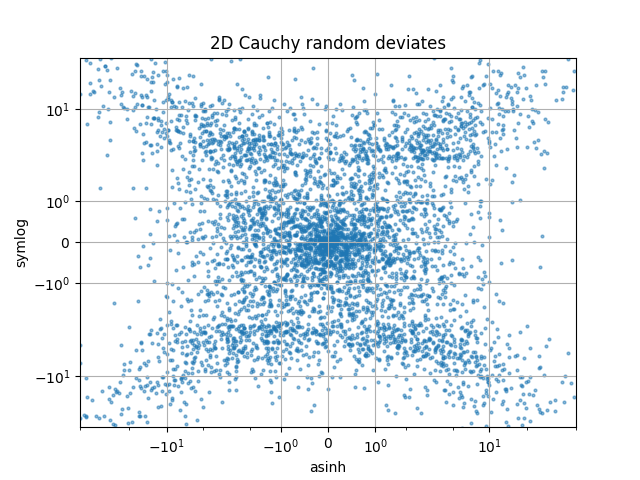
Confronta il ridimensionamento "symlog" e "asinh" su numeri casuali 2D distribuiti da Cauchy, dove si possono vedere artefatti più sottili vicino a y=2 a causa della discontinuità del gradiente in "symlog":

fig3 = plt.figure()
ax = fig3.subplots(1, 1)
r = 3 * np.tan(np.random.uniform(-np.pi / 2.02, np.pi / 2.02,
                                 size=(5000,)))
th = np.random.uniform(0, 2*np.pi, size=r.shape)

ax.scatter(r * np.cos(th), r * np.sin(th), s=4, alpha=0.5)
ax.set_xscale('asinh')
ax.set_yscale('symlog')
ax.set_xlabel('asinh')
ax.set_ylabel('symlog')
ax.set_title('2D Cauchy random deviates')
ax.set_xlim(-50, 50)
ax.set_ylim(-50, 50)
ax.grid()

plt.show()

Riferimenti

Tempo di esecuzione totale dello script: (0 minuti 2,229 secondi)

Galleria generata da Sphinx-Gallery