Istogramma delle serie storiche n.

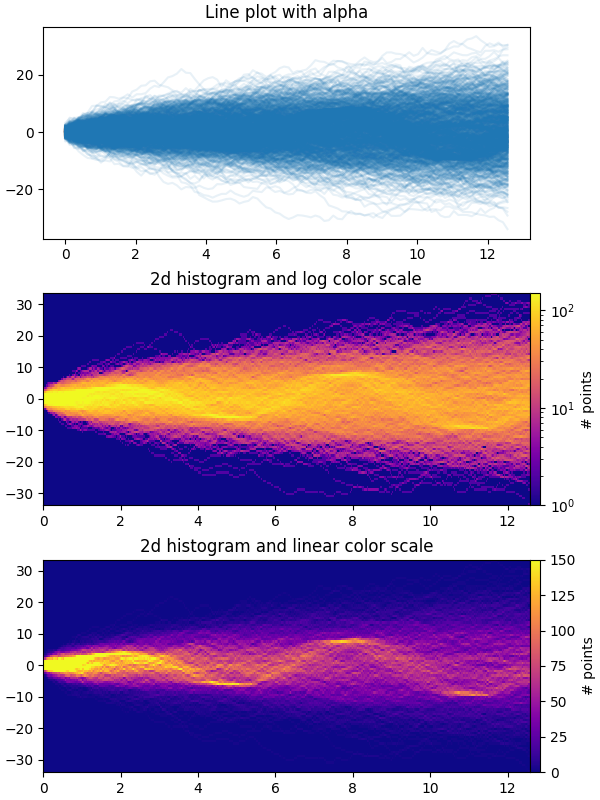
Questo esempio dimostra come visualizzare in modo efficiente un gran numero di serie temporali in un modo che potrebbe potenzialmente rivelare sottostrutture e modelli nascosti che non sono immediatamente evidenti e visualizzarli in modo visivamente accattivante.

In questo esempio, generiamo più serie di "segnali" sinusoidali che sono sepolte sotto un numero maggiore di serie di "rumore/sfondo" a piedi casuali. Per una passeggiata casuale gaussiana imparziale con deviazione standard di σ, la deviazione RMS dall'origine dopo n passaggi è σ*sqrt(n). Quindi, per mantenere le sinusoidi visibili sulla stessa scala delle passeggiate casuali, ridimensioniamo l'ampiezza in base al RMS della passeggiata casuale. Inoltre, introduciamo anche un piccolo offset casuale phi per spostare i seni a sinistra/destra e un po' di rumore casuale additivo per spostare i singoli punti dati su/giù per rendere il segnale un po' più "realistico" (non ti aspetteresti un seno perfetto onda per apparire nei tuoi dati).

Il primo grafico mostra il modo tipico di visualizzare più serie temporali sovrapponendole una sopra l'altra con plt.plotun piccolo valore di alpha. Il secondo e il terzo grafico mostrano come reinterpretare i dati come un istogramma 2d, con interpolazione facoltativa tra punti dati, utilizzando np.histogram2de plt.pcolormesh.

from copy import copy
import time

import numpy as np
import numpy.matlib
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm

fig, axes = plt.subplots(nrows=3, figsize=(6, 8), constrained_layout=True)

# Make some data; a 1D random walk + small fraction of sine waves
num_series = 1000
num_points = 100
SNR = 0.10  # Signal to Noise Ratio
x = np.linspace(0, 4 * np.pi, num_points)
# Generate unbiased Gaussian random walks
Y = np.cumsum(np.random.randn(num_series, num_points), axis=-1)
# Generate sinusoidal signals
num_signal = int(round(SNR * num_series))
phi = (np.pi / 8) * np.random.randn(num_signal, 1)  # small random offset
Y[-num_signal:] = (
    np.sqrt(np.arange(num_points))[None, :]  # random walk RMS scaling factor
    * (np.sin(x[None, :] - phi)
       + 0.05 * np.random.randn(num_signal, num_points))  # small random noise
)


# Plot series using `plot` and a small value of `alpha`. With this view it is
# very difficult to observe the sinusoidal behavior because of how many
# overlapping series there are. It also takes a bit of time to run because so
# many individual artists need to be generated.
tic = time.time()
axes[0].plot(x, Y.T, color="C0", alpha=0.1)
toc = time.time()
axes[0].set_title("Line plot with alpha")
print(f"{toc-tic:.3f} sec. elapsed")


# Now we will convert the multiple time series into a histogram. Not only will
# the hidden signal be more visible, but it is also a much quicker procedure.
tic = time.time()
# Linearly interpolate between the points in each time series
num_fine = 800
x_fine = np.linspace(x.min(), x.max(), num_fine)
y_fine = np.empty((num_series, num_fine), dtype=float)
for i in range(num_series):
    y_fine[i, :] = np.interp(x_fine, x, Y[i, :])
y_fine = y_fine.flatten()
x_fine = np.matlib.repmat(x_fine, num_series, 1).flatten()


# Plot (x, y) points in 2d histogram with log colorscale
# It is pretty evident that there is some kind of structure under the noise
# You can tune vmax to make signal more visible
cmap = copy(plt.cm.plasma)
cmap.set_bad(cmap(0))
h, xedges, yedges = np.histogram2d(x_fine, y_fine, bins=[400, 100])
pcm = axes[1].pcolormesh(xedges, yedges, h.T, cmap=cmap,
                         norm=LogNorm(vmax=1.5e2), rasterized=True)
fig.colorbar(pcm, ax=axes[1], label="# points", pad=0)
axes[1].set_title("2d histogram and log color scale")

# Same data but on linear color scale
pcm = axes[2].pcolormesh(xedges, yedges, h.T, cmap=cmap,
                         vmax=1.5e2, rasterized=True)
fig.colorbar(pcm, ax=axes[2], label="# points", pad=0)
axes[2].set_title("2d histogram and linear color scale")

toc = time.time()
print(f"{toc-tic:.3f} sec. elapsed")
plt.show()

Grafico a linee con alfa, istogramma 2d e scala cromatica logaritmica, istogramma 2d e scala cromatica lineare

0.219 sec. elapsed
0.071 sec. elapsed

Riferimenti

L'uso delle seguenti funzioni, metodi, classi e moduli è mostrato in questo esempio:

Tempo di esecuzione totale dello script: (0 minuti 2,659 secondi)

Galleria generata da Sphinx-Gallery