Utilizzo degli istogrammi per tracciare una distribuzione cumulativa

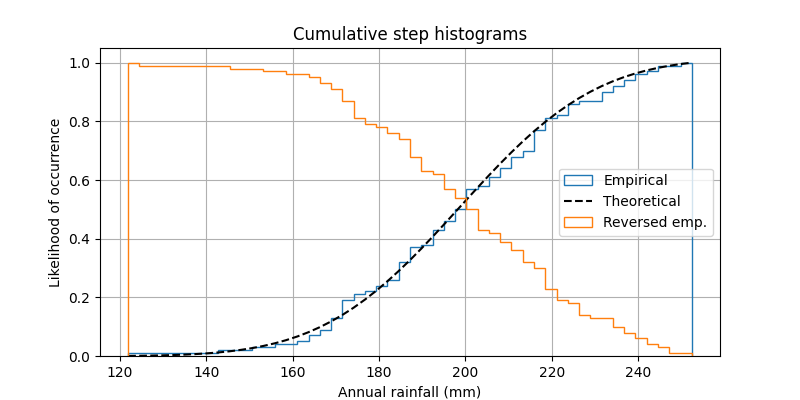
Questo mostra come tracciare un istogramma cumulativo normalizzato come funzione a gradino per visualizzare la funzione di distribuzione cumulativa empirica (CDF) di un campione. Mostriamo anche la CDF teorica.

Vengono mostrate un paio di altre opzioni per la histfunzione. Vale a dire, usiamo il parametro normato per normalizzare l'istogramma e un paio di opzioni diverse per il parametro cumulativo . Il parametro normato assume un valore booleano. Quando True, le altezze dei contenitori vengono ridimensionate in modo tale che l'area totale dell'istogramma sia 1. L' argomento della parola chiave cumulativa è un po' più sfumato. Come normad , puoi passarlo True o False, ma puoi anche passarlo -1 per invertire la distribuzione.

Poiché stiamo mostrando un istogramma normalizzato e cumulativo, queste curve sono effettivamente le funzioni di distribuzione cumulativa (CDF) dei campioni. In ingegneria, le CDF empiriche sono talvolta chiamate curve di "non superamento". In altre parole, puoi guardare il valore y per un dato valore x per ottenere la probabilità e l'osservazione dal campione che non supera quel valore x. Ad esempio, il valore di 225 sull'asse x corrisponde a circa 0,85 sull'asse y, quindi c'è una probabilità dell'85% che un'osservazione nel campione non superi 225. Al contrario, impostando, cumulativea -1 come si fa in l'ultima serie per questo esempio crea una curva di "superamento".

La selezione di conteggi e dimensioni di contenitori diversi può influire in modo significativo sulla forma di un istogramma. I documenti di Astropy hanno un'ottima sezione su come selezionare questi parametri: http://docs.astropy.org/en/stable/visualization/histogram.html

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(19680801)

mu = 200
sigma = 25
n_bins = 50
x = np.random.normal(mu, sigma, size=100)

fig, ax = plt.subplots(figsize=(8, 4))

# plot the cumulative histogram
n, bins, patches = ax.hist(x, n_bins, density=True, histtype='step',
                           cumulative=True, label='Empirical')

# Add a line showing the expected distribution.
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
     np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
y = y.cumsum()
y /= y[-1]

ax.plot(bins, y, 'k--', linewidth=1.5, label='Theoretical')

# Overlay a reversed cumulative histogram.
ax.hist(x, bins=bins, density=True, histtype='step', cumulative=-1,
        label='Reversed emp.')

# tidy up the figure
ax.grid(True)
ax.legend(loc='right')
ax.set_title('Cumulative step histograms')
ax.set_xlabel('Annual rainfall (mm)')
ax.set_ylabel('Likelihood of occurrence')

plt.show()

Riferimenti

L'uso delle seguenti funzioni, metodi, classi e moduli è mostrato in questo esempio:

• matplotlib.axes.Axes.hist/matplotlib.pyplot.hist