Nota
Fare clic qui per scaricare il codice di esempio completo
Scala etichetta angolo invariante #
Questo esempio mostra come creare un'annotazione di angolo invariante di scala. Spesso è utile contrassegnare gli angoli tra le linee o all'interno delle forme con un arco di cerchio. Sebbene Matplotlib fornisca un Arc, un problema intrinseco quando lo si utilizza direttamente per tali scopi è che un arco circolare nello spazio dati non è necessariamente circolare nello spazio di visualizzazione. Inoltre, il raggio dell'arco è spesso meglio definito in un sistema di coordinate che è indipendente dalle coordinate dei dati effettivi, almeno se vuoi essere in grado di ingrandire liberamente il tuo grafico senza che l'annotazione cresca all'infinito.
Ciò richiede una soluzione in cui il centro dell'arco è definito nello spazio dei dati, ma il suo raggio in un'unità fisica come punti o pixel o come rapporto della dimensione degli assi. La AngleAnnotationclasse seguente fornisce tale soluzione.
L'esempio seguente ha due scopi:
Fornisce una soluzione pronta all'uso per il problema di disegnare facilmente angoli nei grafici.
Mostra come creare una sottoclasse di un artista Matplotlib per migliorarne le funzionalità, oltre a fornire un esempio pratico su come utilizzare il sistema di trasformazione di Matplotlib .
Se sei principalmente interessato al primo, puoi copiare la classe sottostante e passare alla sezione Utilizzo .
Classe AngleAnnotation #
L'idea essenziale qui è creare una sottoclasse Arce impostare la sua trasformazione su IdentityTransform, rendendo i parametri dell'arco definiti nello spazio dei pixel. Quindi sovrascriviamo gli Arcattributi _center, theta1,
theta2e widthe heightli rendiamo proprietà, accoppiandoli a metodi interni che calcolano i rispettivi parametri ogni volta che si accede all'attributo e assicurando così che l'arco nello spazio dei pixel rimanga sincronizzato con i punti e le dimensioni di input. Ad esempio, ogni volta che il metodo di disegno dell'arco interroga il suo _center
attributo, invece di ricevere di nuovo lo stesso numero, riceverà invece il risultato del get_center_in_pixelsmetodo che abbiamo definito nella sottoclasse. Questo metodo trasforma il centro in coordinate dati in pixel tramite la trasformazione Axesax.transData. Le dimensioni e gli angoli sono calcolati in modo simile, in modo tale che l'arco cambi automaticamente forma quando, ad esempio, si esegue lo zoom o la panoramica in modo interattivo.
La funzionalità di questa classe permette di annotare l'arco con un testo. Questo testo è Annotationmemorizzato in un attributo text. Poiché la posizione e il raggio dell'arco sono definiti solo al momento del disegno, è necessario aggiornare la posizione del testo di conseguenza. Questo viene fatto reimplementando il metodo Arc's
draw()per consentirgli di chiamare un metodo di aggiornamento per il testo.
L'arco e il testo verranno aggiunti agli Assi forniti all'istanziazione: non è quindi strettamente necessario mantenere un riferimento ad esso.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Arc
from matplotlib.transforms import IdentityTransform, TransformedBbox, Bbox
class AngleAnnotation(Arc):
"""
Draws an arc between two vectors which appears circular in display space.
"""
def __init__(self, xy, p1, p2, size=75, unit="points", ax=None,
text="", textposition="inside", text_kw=None, **kwargs):
"""
Parameters
----------
xy, p1, p2 : tuple or array of two floats
Center position and two points. Angle annotation is drawn between
the two vectors connecting *p1* and *p2* with *xy*, respectively.
Units are data coordinates.
size : float
Diameter of the angle annotation in units specified by *unit*.
unit : str
One of the following strings to specify the unit of *size*:
* "pixels": pixels
* "points": points, use points instead of pixels to not have a
dependence on the DPI
* "axes width", "axes height": relative units of Axes width, height
* "axes min", "axes max": minimum or maximum of relative Axes
width, height
ax : `matplotlib.axes.Axes`
The Axes to add the angle annotation to.
text : str
The text to mark the angle with.
textposition : {"inside", "outside", "edge"}
Whether to show the text in- or outside the arc. "edge" can be used
for custom positions anchored at the arc's edge.
text_kw : dict
Dictionary of arguments passed to the Annotation.
**kwargs
Further parameters are passed to `matplotlib.patches.Arc`. Use this
to specify, color, linewidth etc. of the arc.
"""
self.ax = ax or plt.gca()
self._xydata = xy # in data coordinates
self.vec1 = p1
self.vec2 = p2
self.size = size
self.unit = unit
self.textposition = textposition
super().__init__(self._xydata, size, size, angle=0.0,
theta1=self.theta1, theta2=self.theta2, **kwargs)
self.set_transform(IdentityTransform())
self.ax.add_patch(self)
self.kw = dict(ha="center", va="center",
xycoords=IdentityTransform(),
xytext=(0, 0), textcoords="offset points",
annotation_clip=True)
self.kw.update(text_kw or {})
self.text = ax.annotate(text, xy=self._center, **self.kw)
def get_size(self):
factor = 1.
if self.unit == "points":
factor = self.ax.figure.dpi / 72.
elif self.unit[:4] == "axes":
b = TransformedBbox(Bbox.unit(), self.ax.transAxes)
dic = {"max": max(b.width, b.height),
"min": min(b.width, b.height),
"width": b.width, "height": b.height}
factor = dic[self.unit[5:]]
return self.size * factor
def set_size(self, size):
self.size = size
def get_center_in_pixels(self):
"""return center in pixels"""
return self.ax.transData.transform(self._xydata)
def set_center(self, xy):
"""set center in data coordinates"""
self._xydata = xy
def get_theta(self, vec):
vec_in_pixels = self.ax.transData.transform(vec) - self._center
return np.rad2deg(np.arctan2(vec_in_pixels[1], vec_in_pixels[0]))
def get_theta1(self):
return self.get_theta(self.vec1)
def get_theta2(self):
return self.get_theta(self.vec2)
def set_theta(self, angle):
pass
# Redefine attributes of the Arc to always give values in pixel space
_center = property(get_center_in_pixels, set_center)
theta1 = property(get_theta1, set_theta)
theta2 = property(get_theta2, set_theta)
width = property(get_size, set_size)
height = property(get_size, set_size)
# The following two methods are needed to update the text position.
def draw(self, renderer):
self.update_text()
super().draw(renderer)
def update_text(self):
c = self._center
s = self.get_size()
angle_span = (self.theta2 - self.theta1) % 360
angle = np.deg2rad(self.theta1 + angle_span / 2)
r = s / 2
if self.textposition == "inside":
r = s / np.interp(angle_span, [60, 90, 135, 180],
[3.3, 3.5, 3.8, 4])
self.text.xy = c + r * np.array([np.cos(angle), np.sin(angle)])
if self.textposition == "outside":
def R90(a, r, w, h):
if a < np.arctan(h/2/(r+w/2)):
return np.sqrt((r+w/2)**2 + (np.tan(a)*(r+w/2))**2)
else:
c = np.sqrt((w/2)**2+(h/2)**2)
T = np.arcsin(c * np.cos(np.pi/2 - a + np.arcsin(h/2/c))/r)
xy = r * np.array([np.cos(a + T), np.sin(a + T)])
xy += np.array([w/2, h/2])
return np.sqrt(np.sum(xy**2))
def R(a, r, w, h):
aa = (a % (np.pi/4))*((a % (np.pi/2)) <= np.pi/4) + \
(np.pi/4 - (a % (np.pi/4)))*((a % (np.pi/2)) >= np.pi/4)
return R90(aa, r, *[w, h][::int(np.sign(np.cos(2*a)))])
bbox = self.text.get_window_extent()
X = R(angle, r, bbox.width, bbox.height)
trans = self.ax.figure.dpi_scale_trans.inverted()
offs = trans.transform(((X-s/2), 0))[0] * 72
self.text.set_position([offs*np.cos(angle), offs*np.sin(angle)])
Utilizzo n.
Gli argomenti richiesti AngleAnnotationsono il centro dell'arco, xy e due punti, in modo tale che l'arco si estenda tra i due vettori che collegano
p1 e p2 con xy , rispettivamente. Quelli sono dati in coordinate di dati. Ulteriori argomenti sono la dimensione dell'arco e la sua unità . Inoltre, è possibile specificare un
testo , che verrà disegnato all'interno o all'esterno dell'arco, in base al valore di textposition . L'utilizzo di questi argomenti è mostrato di seguito.
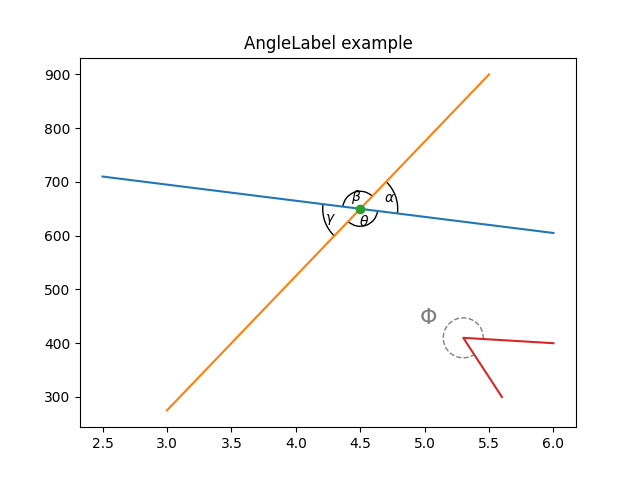
fig, ax = plt.subplots()
fig.canvas.draw() # Need to draw the figure to define renderer
ax.set_title("AngleLabel example")
# Plot two crossing lines and label each angle between them with the above
# ``AngleAnnotation`` tool.
center = (4.5, 650)
p1 = [(2.5, 710), (6.0, 605)]
p2 = [(3.0, 275), (5.5, 900)]
line1, = ax.plot(*zip(*p1))
line2, = ax.plot(*zip(*p2))
point, = ax.plot(*center, marker="o")
am1 = AngleAnnotation(center, p1[1], p2[1], ax=ax, size=75, text=r"$\alpha$")
am2 = AngleAnnotation(center, p2[1], p1[0], ax=ax, size=35, text=r"$\beta$")
am3 = AngleAnnotation(center, p1[0], p2[0], ax=ax, size=75, text=r"$\gamma$")
am4 = AngleAnnotation(center, p2[0], p1[1], ax=ax, size=35, text=r"$\theta$")
# Showcase some styling options for the angle arc, as well as the text.
p = [(6.0, 400), (5.3, 410), (5.6, 300)]
ax.plot(*zip(*p))
am5 = AngleAnnotation(p[1], p[0], p[2], ax=ax, size=40, text=r"$\Phi$",
linestyle="--", color="gray", textposition="outside",
text_kw=dict(fontsize=16, color="gray"))
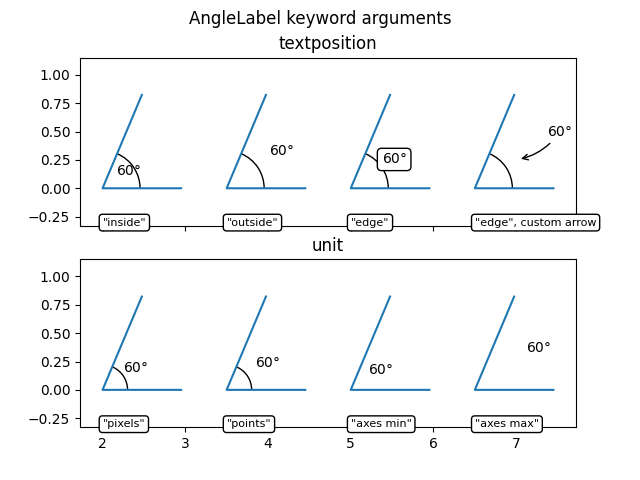
AngleLabelopzioni #
Gli argomenti della parola chiave textposition e unit possono essere utilizzati per modificare la posizione dell'etichetta di testo, come mostrato di seguito:
# Helper function to draw angle easily.
def plot_angle(ax, pos, angle, length=0.95, acol="C0", **kwargs):
vec2 = np.array([np.cos(np.deg2rad(angle)), np.sin(np.deg2rad(angle))])
xy = np.c_[[length, 0], [0, 0], vec2*length].T + np.array(pos)
ax.plot(*xy.T, color=acol)
return AngleAnnotation(pos, xy[0], xy[2], ax=ax, **kwargs)
fig, (ax1, ax2) = plt.subplots(nrows=2, sharex=True)
fig.suptitle("AngleLabel keyword arguments")
fig.canvas.draw() # Need to draw the figure to define renderer
# Showcase different text positions.
ax1.margins(y=0.4)
ax1.set_title("textposition")
kw = dict(size=75, unit="points", text=r"$60°$")
am6 = plot_angle(ax1, (2.0, 0), 60, textposition="inside", **kw)
am7 = plot_angle(ax1, (3.5, 0), 60, textposition="outside", **kw)
am8 = plot_angle(ax1, (5.0, 0), 60, textposition="edge",
text_kw=dict(bbox=dict(boxstyle="round", fc="w")), **kw)
am9 = plot_angle(ax1, (6.5, 0), 60, textposition="edge",
text_kw=dict(xytext=(30, 20), arrowprops=dict(arrowstyle="->",
connectionstyle="arc3,rad=-0.2")), **kw)
for x, text in zip([2.0, 3.5, 5.0, 6.5], ['"inside"', '"outside"', '"edge"',
'"edge", custom arrow']):
ax1.annotate(text, xy=(x, 0), xycoords=ax1.get_xaxis_transform(),
bbox=dict(boxstyle="round", fc="w"), ha="left", fontsize=8,
annotation_clip=True)
# Showcase different size units. The effect of this can best be observed
# by interactively changing the figure size
ax2.margins(y=0.4)
ax2.set_title("unit")
kw = dict(text=r"$60°$", textposition="outside")
am10 = plot_angle(ax2, (2.0, 0), 60, size=50, unit="pixels", **kw)
am11 = plot_angle(ax2, (3.5, 0), 60, size=50, unit="points", **kw)
am12 = plot_angle(ax2, (5.0, 0), 60, size=0.25, unit="axes min", **kw)
am13 = plot_angle(ax2, (6.5, 0), 60, size=0.25, unit="axes max", **kw)
for x, text in zip([2.0, 3.5, 5.0, 6.5], ['"pixels"', '"points"',
'"axes min"', '"axes max"']):
ax2.annotate(text, xy=(x, 0), xycoords=ax2.get_xaxis_transform(),
bbox=dict(boxstyle="round", fc="w"), ha="left", fontsize=8,
annotation_clip=True)
plt.show()
Riferimenti
L'uso delle seguenti funzioni, metodi, classi e moduli è mostrato in questo esempio:
Tempo di esecuzione totale dello script: (0 minuti 1.034 secondi)